如图1,的三个顶点、、分别落在抛物线的图象上,点的横坐标为,点的纵坐标为.(点在点的左侧)
(1)求点、的坐标;
(2)将绕点逆时针旋转得到△,抛物线经过、两点,已知点为抛物线的对称轴上一定点,且点恰好在以为直径的圆上,连接、,求△的面积;
(3)如图2,延长交抛物线于点,连接,在坐标轴上是否存在点,使得以、、为顶点的三角形与△相似.若存在,请求出点的坐标;若不存在,请说明理由.

如图,在△ABC中,∠ B=90°,AB=6cm,BC=8cm,点P从点A出发沿AB边向点B以1cm/秒的速度移动,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.
如果P、Q分别从A、B同时出发,经过多长时间,使△PBQ的面积为8cm2?
如果P、Q分别从A、B同时出发, 当P、Q两点运动几秒时,
 有最小值,并求这个最小值.
有最小值,并求这个最小值.
如图所示,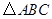 是直角三角形,
是直角三角形,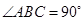 ,以
,以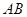 为直径的⊙O交
为直径的⊙O交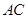 于点
于点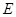 ,点
,点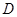 是
是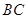 边的中点,连结
边的中点,连结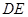 .
.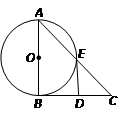
求证:
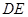 与⊙O相切
与⊙O相切若⊙O的半径为
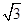 ,
,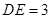 ,求
,求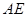 .
.
大家一定熟知杨辉三角(Ⅰ),观察下列等式(Ⅱ)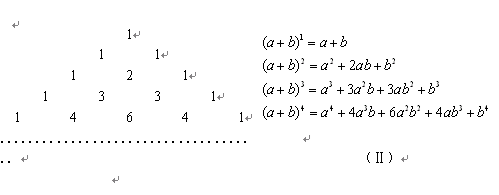
根据前面各式规律,则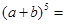 .
.
已知如图,矩形OABC的长OA= ,宽OC=1,
,宽OC=1,
将△AOC沿AC翻折得△APC.
求∠PCB的度数
若P,A两点在抛物线y=-
 x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;(2)中的抛物线与矩形OABC边CB相交于点D,与x轴相交于另外一点E,若点M是x轴上的点,N是y轴上的点,以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标.
如图,抛物线 (a
(a 0)与反比例函数
0)与反比例函数 的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
求反比例函数的解析式
用含t的代数式表示直线AB的解析式;
求抛物线的解析式;
过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,把△AOB绕点O逆时针旋转90º,请在图②中画出旋转后的三角形,并直接写出所有满足△EOC∽△AOB的点E的坐标.