如图①,在平面直角坐标系中,已知,,,四点,动点以每秒个单位长度的速度沿运动不与点、点重合),设运动时间为(秒.
(1)求经过、、三点的抛物线的解析式;
(2)点在(1)中的抛物线上,当为的中点时,若,求点的坐标;
(3)当在上运动时,如图②.过点作轴,垂足为,,垂足为.设矩形与重叠部分的面积为,求与的函数关系式,并求出的最大值;
(4)点为轴上一点,直线与直线交于点,与轴交于点.是否存在点,使得为等腰三角形?若存在,直接写出符合条件的所有点的坐标;若不存在,请说明理由.

如图:已知AB是⊙O的直径,P为AB的延长线上一点.且BP=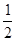 AB,C、D是半圆AB的两个三等分点,连接PD.
AB,C、D是半圆AB的两个三等分点,连接PD.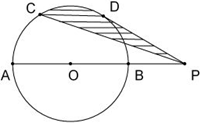
(1)PD与⊙O有怎样的位置关系?并证明你的结论;
(2)连接PC,若AB=10cm,求由PC,弧CD、PD所围成的图形的面积(结果保留π).
先阅读理解下面的例题,再按要求解答后面的问题
例题:解一元二次不等式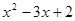 >0.解:令y=
>0.解:令y=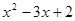 ,画出y=
,画出y=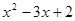 如图所示,
如图所示,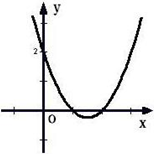
由图像可知:当x<1或x>2时,y>0.所以一元二次不等式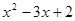 >0的解集为x<1或x>2.
>0的解集为x<1或x>2.
填空:(1)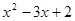 <0的解集为;
<0的解集为;
(2)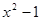 >0的解集为;
>0的解集为;
用类似的方法解一元二次不等式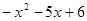 >0.
>0.
如图,在矩形ABCD(AB<AD)中,将△ABE沿AE对折,使AB边落在对角线AC上,点B的对应点为F,同时将△CEG沿EG对折,使CE边落在EF所在直线上,点C的对应点为H.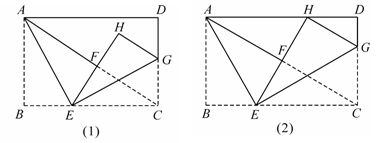
(1)证明:AF∥HG(图(1));
(2)如果点C的对应点H恰好落在边AD上(图(2)).判断四边形AECH的形状,并说明理由.
甲、乙两人准备整理一批新到的实验器材.若甲单独整理需要40分钟完工;若甲、乙 共同整理20分钟后,乙需再单独整理20分钟才能完工.
(1)问乙单独整理多少分钟完工?
(2)若乙因工作需要,他的整理时间不超过30分钟,则甲至少整理多少分钟才能完工?
要了解某地区九年级学生的身高情况,从中随机抽取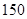 名学生的身高作为一个样本,身高均在
名学生的身高作为一个样本,身高均在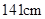 ~
~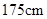 之间(取整数厘米),整理后分成
之间(取整数厘米),整理后分成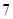 组,绘制出频数分布直方图(不完整).根据图中提供的信息,解答下列问题:
组,绘制出频数分布直方图(不完整).根据图中提供的信息,解答下列问题: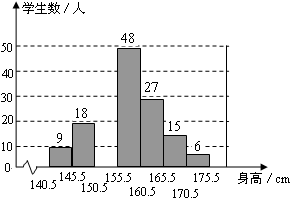
(1)补全频数分布直方图;
(2)抽取的样本中,学生身高的中位数在哪个小组?
(3)该地区共有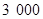 名九年级学生,估计其中身高不低于
名九年级学生,估计其中身高不低于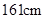 的人数.
的人数.