如图,在中,,以为直径的交于点,连接,过点作,垂足为,、的延长线交于点.
(1)求证:是的切线;
(2)求证:;
(3)若,,求的长.
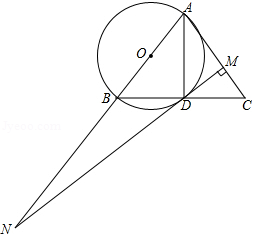
证明:(1)如图,连接,
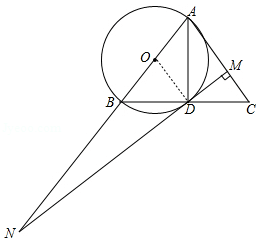
是直径,
,
又,
,,
,,
,
,
,
又是半径,
是的切线;
(2),
,
,,
,
,
,
又,
,
,
;
(3),,
,
,
,
,
,
,
,
,,
,
,
,
.
某工厂现有甲种原料380千克,乙种原料290千克,计划用这两种原料生产A,B两种产品共50件,已知生产1件A种产品需甲种原料9千克,乙种原料3千克,可获利700元;生产1件B种产品需甲种原料4千克,乙种原料10千克,可获利1200元,设工厂生产A,B两种产品可获总利润是y元,其中甲种产品的生产件数是x,
(1)写出y与x之间的函数关系式;
(2)如何安排A,B两种产品的生产件数,使总利润y有最大值,并求出y的最大值。
有两个同学做了一个数字游戏:有三张正面写有数字-1,0,1的卡片片它们背面完全相同,将这三张卡片背面朝上洗匀后,其中一个同学随机抽取一张,将其正面的数字作为p的值,然后将卡片放回洗匀,另一个同学再从这三张卡片中随机抽取一张,将其正面的数字作为q的值,两次结果记为(p,q)
(1)请用树状图或列表法表示(p,q)所有可能出现的结果;
(2)求满足关于x的方程x2+px+q=0没有实数根的概率。
(1)计算: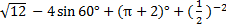 ;
;
(2)化简: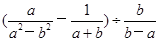
如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.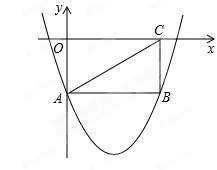
(1)求A点坐标及线段AB的长;
(2)若点P由点A出发以每秒1个单位的速度沿AB边向点B移动,1秒后点Q也由点A出发以每秒7个单位的速度沿A-O-C-B的方向向点B移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒.
①当PQ⊥AC时,求t的值;
②当PQ∥AC时,对于抛物线对称轴上一点H,当点H的纵坐标满足条件_________时,∠HOQ<∠POQ.(直接写出答案)
在△ABC中,∠ACB=90°,∠A<45°,点O为AB中点,一个足够大的三角板的直角顶点与点O重合,一边OE经过点C,另一边OD与AC交于点M.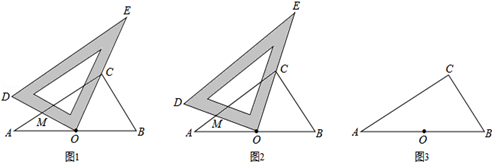
(1)如图1,当∠A=30°时,求证:MC2=AM2+BC2;
(2)如图2,当∠A≠30°时,(1)中的结论是否成立?如果成立,请说明理由;如果不成立,请写出你认为正确的结论,并说明理由;
(3)将三角形ODE绕点O旋转,若直线OD与直线AC相交于点M,直线OE与直线BC相交于点N,连接MN,则MN2=AM2+BN2成立吗?答:(填“成立”或“不成立”)