如图,在菱形 中,点 在 轴上,点 的坐标为 , ,将菱形绕点 旋转,当点 落在 轴上时,点 的对应点的坐标为
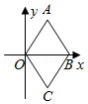
| A. |
或 , |
B. |
, |
| C. |
, |
D. |
或 , |
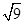 的值等于()
的值等于()
| A.3 | B.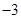 |
C.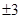 |
D.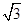 |
从3,4,5这三个数中任取两个,分别记作p和q(p≠q),构造函数y=px-2和y=x+q,使这两个函数图象交点的横坐标始终小于2,则这样的有序数组(p,q)共有().
| A.2对 | B.3对 | C.4对 | D.5对 |
如果 ,
,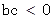 ,则函数
,则函数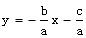 的图象一定不经过()
的图象一定不经过()
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
在边长为2的正三角形ABC中,已知点P是三角形内任意一点,则点P到三角形的三边距离之和PD+PE+PF等于()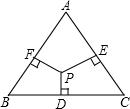
A.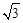 |
B.2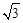 |
C.4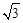 |
D.无法确定 |
已知等腰三角形的一个内角等于50º,则该三角形的一个底角的余角是()
| A.25º | B.40º或30º | C.25º或40º | D.50º |