,两城市之间有一条公路相连,公路中途穿过市,甲车从市到市,乙车从市到市,甲车的速度比乙车的速度慢20千米时,两车距离市的路程(单位:千米)与驶的时间(单位:小时)的函数图象如图所示,结合图象信息,解答下列问题:
(1)甲车的速度是 千米时,在图中括号内填入正确的数;
(2)求图象中线段所在直线的函数解析式,不需要写出自变量的取值范围;
(3)直接写出甲车出发后几小时,两车距市的路程之和是460千米.

我镇绿色和特色农产品在市场上颇具竞争力.外贸商胡经理按市场价格10元/千克在我区收购了6000千克蘑菇存放入冷库中.请根据胡经理提供的预测信息(如图)帮胡经理解决以下问题: 
(1)若胡经理想将这批蘑菇存放x天后一次性出售, 则x天后这批蘑菇的销售单价为元, 这批蘑菇的销售量是千克;
(2)胡经理将这批蘑菇存放多少天后,一次性出售所得的销售总金额为100000元;(销售总金额=销售单价×销售量).
(3)将这批蘑菇存放多少天后一次性出售可获得最大利润?最大利润是多少?
如图, △ABC内接于⊙O, AD⊥BC于D, AE是⊙O的直径. 若AB=6, AC="8," AE="11," 求AD的长.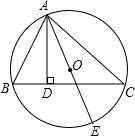
将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面
(1)从中随机抽出一张牌,试求出牌面数字是偶数的概率;
(2)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率.
网格中每个小正方形的边长都是1.
(1)将图①中的格点三角形ABC平移,使点A平移至点A`,画出平移后的三角形;
(2)在图②中画一个格点三角形DEF,使△DEF∽△ABC,且相似比为2∶1;
(3)在图③中画一个格点三角形PQR,使△PQR∽△ABC,且相似比为 ∶1.
∶1.
如图,圆心角∠AOB=120°,弦AB=2 cm.
cm.
(1)求⊙O的半径r;
(2)求劣弧 的长(结果保留
的长(结果保留 ).
).