某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜,某超市看好甲、乙两种有机蔬菜的市场价值,经调查甲种蔬菜进价每千克元,售价每千克16元;乙种蔬菜进价每千克元,售价每千克18元.
(1)该超市购进甲种蔬菜15千克和乙种蔬菜20千克需要430元;购进甲种蔬菜10千克和乙种蔬菜8千克需要212元,求,的值.
(2)该超市决定每天购进甲、乙两种蔬菜共100千克,且投入资金不少于1160元又不多于1168元,设购买甲种蔬菜千克为正整数),求有哪几种购买方案.
(3)在(2)的条件下,超市在获得的利润取得最大值时,决定售出的甲种蔬菜每千克捐出元,乙种蔬菜每千克捐出元给当地福利院,若要保证捐款后的利润率不低于,求的最大值.
如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为18°,且OA=OB=3m.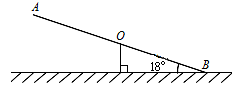
(1)求此时另一端A离地面的距离(结果精确到0.1);
(2)跷动AB,使端点A碰到地面,请画出点A运动的路线(保留画图痕迹),并求出点A运动路线的长.(结果保留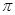 )(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
)(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
(1)计算: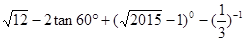 ;
;
(2)化简: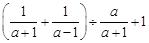 .
.
如图,抛物线y=ax2+bx(a>0)与双曲线y= 相交于点A,B.已知点B的坐标为(﹣2,﹣2),点A在第一象限内,且tan∠AOx=4.过点A作直线AC∥x轴,交抛物线于另一点C.
相交于点A,B.已知点B的坐标为(﹣2,﹣2),点A在第一象限内,且tan∠AOx=4.过点A作直线AC∥x轴,交抛物线于另一点C.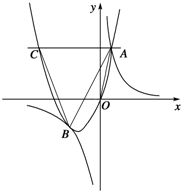
(1)求双曲线和抛物线的解析式;
(2)计算△ABC的面积;
(3)在抛物线上是否存在点D,使△ABD的面积等于△ABC的面积.若存在,请你写出点D的坐标;若不存在,请你说明理由.
如图,在矩形ABCD中,AD=4,AB=m(m>4),点P是AB边上的任意一点(不与A、B重合),连结PD,过点P作PQ⊥PD,交直线BC于点Q.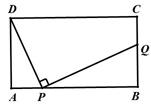
(1)当m=10时,是否存在点P使得点Q与点C重合?若存在,求出此时AP的长;若不存在,说明理由;
(2)连结AC,若PQ∥AC,求线段BQ的长(用含m的代数式表示)
(3)若△PQD为等腰三角形,求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式,并写出m的取值范围.
如图,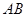 是
是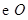 的直径,
的直径,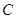 为圆周上一点,
为圆周上一点,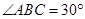 ,
,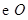 过点
过点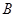 的切线与
的切线与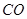 的延长线交于点
的延长线交于点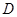 .
.
求证:(1)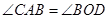 ;
;
(2)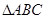 ≌
≌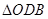 .
.