由若干个相同的小立方体搭成的几何体的三视图如图所示,则搭成这个几何体的小立方体的个数是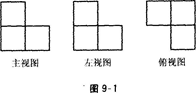
| A.3个 | B.4个 | C.5个 | D.6个 |
温家宝总理在2009年政府工作报告中提出,今后三年内各级政府拟投入医疗卫生领域的资金将达到8500亿元人民币,用科学记数法表示“8500亿”为
| A.85×1010 | B.8.5×1010 | C.8.5×1011 | D.0.85×1012 |
下列各组数中,互为相反数的是
A.2和 |
B.-2和- |
C.-2和︱-2︱ | D.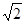 和 和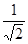 |
△ABC中,∠B=90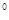 ,∠C=30
,∠C=30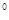 ,AB=1,△ABC关于A成中心对称的三角形记为△ADE,则CE的长是()
,AB=1,△ABC关于A成中心对称的三角形记为△ADE,则CE的长是()
A.2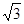 |
B. 2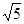 |
C. 4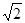 |
D. 4 |
旋转后得到的图形与原图形相比 ()
A形状和大小都发生变化 B形状不变,大小发生变化
C形状改变,大小不变 D形状和大小都不发生变化