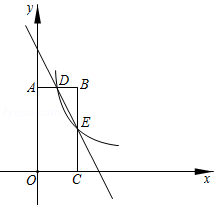
如图,在矩形中,,,点是边的中点,反比例函数的图象经过点,交边于点,直线的解析式为.
(1)求反比例函数的解析式和直线的解析式;
(2)在轴上找一点,使的周长最小,求出此时点的坐标;
(3)在(2)的条件下,的周长最小值是 .
解不等式组: 把它的解集在数轴上表示出
把它的解集在数轴上表示出 来,并求它的整数解.
来,并求它的整数解.
(本题满分14分,第(1)题4分,第(2)题4分,第(2)题6分)
在梯形ABCD中,AD//BC,AB⊥AD,AB=4,AD=5,CD=5.E为底边BC上一点,以点E为圆心,BE为半径画⊙E交直线DE于点F.
(1)如图,当点F在线段DE上时,设BE ,DF
,DF ,试建立
,试建立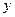 关于
关于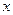 的函数关系式,
的函数关系式,
并写出自变量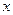 的取值范围;
的取值范围;
(2)当以CD直径的⊙O与⊙E与相切时,求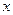 的值;
的值;
(3)联接AF、BF,当△ABF是以AF为腰的等腰三角形时,求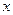 的值。
的值。
(本题满分12分,第(1)、(2)题各6分)
如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C, D为OC的中点,直线AD交抛物线于点E(2,6),且△ABE与△ABC的面积之比为3∶2.
(1)求直线AD和抛物线的解析式;
(2)抛物线的对称轴与 轴相交于点F,点Q为直线AD上一点,且△ABQ与△ADF相似,直接写出点Q点的坐标.
轴相交于点F,点Q为直线AD上一点,且△ABQ与△ADF相似,直接写出点Q点的坐标.
(本题满分12分,第(1)题7分,第(2)题5分)
如图,在⊙O中,直径AB与弦CD垂直,垂 足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.
足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.
(1)证明:直线FC与⊙O相切;
(2)若 ,求证:四边形OCBD是菱形.
,求证:四边形OCBD是菱形.

(本题满分10分,第(1)小题4分,第(2)小题6分)
如图,正方形ABCD中, M是边BC上一点,且BM =
=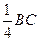 .
.
(1)若
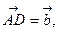 试用
试用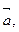
 表示
表示 ;
;
(2)若AB=4
|
|
,求sin∠AMD的值.

