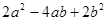如图,已知AB//CD,试问:∠1、∠2、∠3有什么关系?请证明你的结论。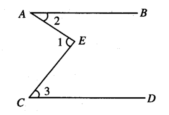
某服装专卖店老板对第一季度男、女服装的销售收入进行统计,并绘制了扇形统计图(如图)。由于三月份开展促销活动,男、女服装的销售收入分别比二月份增长了40%和64%,已知第一季度男女服装的销售总收入为20万元。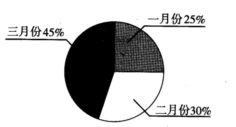
(1)一月份销售收入为_____________万元,
二月份销售收入为___________万元,
三月份销售收入为___________万元,
(2)列方程(组)求二月份男、女服装的销售收入分别是多少万元?
填空题:如图,AB//CD,∠ABC=50°,∠CPN=150°,∠PNB=60°,∠NDC=60°,求∠BCP的度数。
解: ,(已知)
,(已知)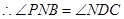 ,(等量代换)
,(等量代换) ___________//__________,()
___________//__________,() _________=180°,()
_________=180°,()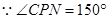 ,(已知)
,(已知)
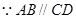 ,(已知)
,(已知)
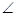 ____________,()
____________,() ,(已知)
,(已知) __________,(等量代换)
__________,(等量代换)
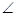 BCP=
BCP=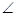 BCD-
BCD-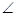 PCD=____________°-________°=_________°
PCD=____________°-________°=_________°
因式分解: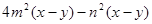
因式分解: