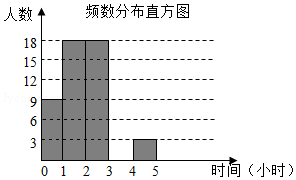
某校为了了解全校学生线上学习情况，随机选取该校部分学生，调查学生居家学习时每天学习时间（包括线上听课及完成作业时间）．如图是根据调查结果绘制的统计图表．请你根据图表中的信息完成下列问题：

频数分布表

学习时间分组	频数	频率
$A$组$(0⩽x<1)$	9	$m$
$B$组$(1⩽x<2)$	18	0.3
$C$组$(2⩽x<3)$	18	0.3
$D$组$(3⩽x<4)$	$n$	0.2
$E$组$(4⩽x<5)$	3	0.05

（1）频数分布表中$m=$　　，$n=$　　，并将频数分布直方图补充完整；

（2）若该校有学生1000名，现要对每天学习时间低于2小时的学生进行提醒，根据调查结果，估计全校需要提醒的学生有多少名？

（3）已知调查的$E$组学生中有2名男生1名女生，老师随机从中选取2名学生进一步了解学生居家学习情况．请用树状图或列表求所选2名学生恰为一男生一女生的概率．

科目 数学   题型 解答题   难度 中等

知识点： 用样本估计总体 列表法与树状图法 频数（率）分布表 频数（率）分布直方图