九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究了函数 的图象与性质共探究过程如下:
(1)绘制函数图象,如图1.
列表:下表是 与 的几组对应值,其中 ;
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
1 |
2 |
4 |
4 |
2 |
|
|
|
描点:根据表中各组对应值 ,在平面直角坐标系中描出了各点;
连线:用平滑的曲线顺次连接各点,画出了部分图象.请你把图象补充完整;
(2)通过观察图1,写出该函数的两条性质;
① ;
② ;
(3)①观察发现:如图2.若直线 交函数 的图象于 , 两点,连接 ,过点 作 交 轴于 .则 ;
②探究思考:将①中"直线 "改为"直线 ",其他条件不变,则 ;
③类比猜想:若直线 交函数 的图象于 , 两点,连接 ,过点 作 交 轴于 ,则 .

如图所示,直线AB与x轴交于点A,与y轴交于点C(0,2),且与反比例函数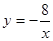 的图象在第二象限内交于点B,过点B作BD⊥x轴于点D,OD=2.
的图象在第二象限内交于点B,过点B作BD⊥x轴于点D,OD=2.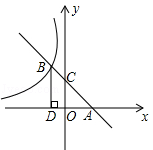
(1)求直线AB的解析式;
(2)若点P是线段BD上一点,且△PBC的面积等于3,求点P的坐标.
如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE与G点,交DF与F点,CE交DF于H点、交BE于E点.求证:△EBC≌△FDA.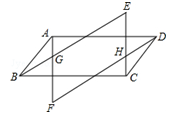
(1)解不等式组: .
.
(2)计算: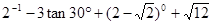
分解因式: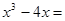 .
.
已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点为N(0,6),且与x轴交于A、B两点.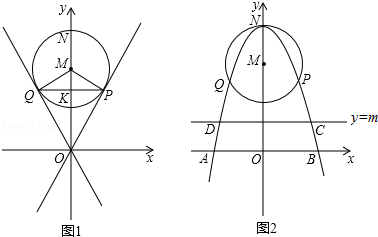
(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).