勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有"若勾三,股四,则弦五"的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅"弦图"(如图 ,后人称之为"赵爽弦图",流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)

(2)①如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足 的有 个;

②如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为 , ,直角三角形面积为 ,请判断 , , 的关系并证明;
(3)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图8所示的"勾股树".在如图9所示的"勾股树"的某部分图形中,设大正方形 的边长为定值 ,四个小正方形 , , , 的边长分别为 , , , ,已知 ,则当 变化时,回答下列问题:(结果可用含 的式子表示)
① ;
② 与 的关系为 , 与 的关系为 .
(·辽宁葫芦岛)小明开了一家网店,进行社会实践,计划经销甲、乙两种商品.若甲商品每件利润10元,乙商品每件利润20元,则每周能卖出甲商品40件,乙商品20件.经调查,甲、乙两种商品零售单价分别每降价1元,这两种商品每周可各多销售10件.为了提高销售量,小明决定把甲、乙两种商品的零售单价都降价x元.
(1)直接写出甲、乙两种商品每周的销售量y(件)与降价x(元)之间的函数关系式:y甲= ,y乙= ;
(2)求出小明每周销售甲、乙两种商品获得的总利润W(元)与降价x(元)之间的函数关系式?如果每周甲商品的销售量不低于乙商品的销售量的 ,那么当x定为多少元时,才能使小明每周销售甲、乙两种商品获得的总利润最大?
,那么当x定为多少元时,才能使小明每周销售甲、乙两种商品获得的总利润最大?
(·辽宁葫芦岛)某中学要进行理、化实验加试,需用九年级两个班级的学生整理实验器材.已知一班单独整理需要30分钟完成.
(1)如果一班与二班共同整理15分钟后,一班另有任务需要离开,剩余工作由二班单独整理15分钟才完成任务,求二班单独整理这批实验器材需要多少分钟?
(2)如果一、二的工作效率不变,先由二班单独整理,时间不超过20分钟,剩余工作再由一班独立完成,那么整理完这批器材一班至少还需要多少分钟?
(·黑龙江绥化)自学下面材料后,解答问题。
分母中含有未知数的不等式叫分式不等式。如: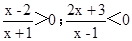 等 。那么如何求出它们的解集呢?
等 。那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负。其字母表达式为:
(1)若a>0 ,b>0 ,则 >0;若a<0 ,b<0,则
>0;若a<0 ,b<0,则 >0;
>0;
(2)若a>0 ,b<0 ,则 <0 ;若a<0,b>0 ,则
<0 ;若a<0,b>0 ,则 <0。
<0。
反之:(1)若 >0则
>0则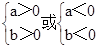
(2)若 <0 ,则__________或_____________.
<0 ,则__________或_____________.
根据上述规律,求不等式 的解集。
的解集。
(·辽宁沈阳)如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B的坐标为(60,0),OA=AB,∠OAB=90°,OC=50.点P是线段OB上的一个动点(点P不与点O、B重合),过点P与y轴平行的直线l交边OA或边AB于点Q,交边OC或边BC于点R,设点P横坐标为t,线段QR的长度为m.已知t=40时,直线l恰好经过点C.
(1)求点A和点C的坐标;
(2)当0<t<30时,求m关于t的函数关系式;
(3)当m=35时,请直接写出t的值;
(4)直线l上有一点M,当∠PMB+∠POC=90°,且△PMB的周长为60时,请直接写出满足条件的点M的坐标.
(·辽宁丹东)如图,线段AB,CD表示甲、乙两幢居民楼的高,两楼间的距离BD是60米.某人站在A处测得C点的俯角为37°,D点的俯角为48°(人的身高忽略不计),求乙楼的高度CD.