如图,在 中, ,以 为直径的 交 于点 , 与过点 的切线互相垂直,垂足为 .
(1)求证: 平分 ;
(2)若 ,求 的值.

(·湖南株洲)P表示 边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么P与
边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么P与 的关系式是:
的关系式是: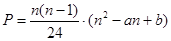
 (其中,
(其中,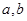 是常数,
是常数,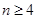 )
)
(1)填空:通过画图可得:四边形时,P= (填数字),五边形时,,P= (填数字)
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求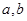 的值
的值
(注:本题的多边形均指凸多边形)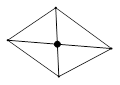
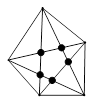
(·湖南长沙)在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”。
(1)求函数y=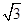 x+2的图像上所有“中国结”的坐标;
x+2的图像上所有“中国结”的坐标;
(2)求函数y= (k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(3)若二次函数y=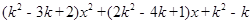 (k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图像与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
(k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图像与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
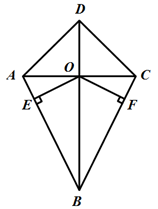
(·湖北孝感)我们把两组邻边相等的四边形叫做“筝形”.如图,四边形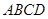 是一个筝形,其中
是一个筝形,其中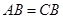 ,
,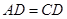 .对角线
.对角线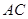 ,
,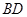 相交于点
相交于点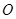 ,
,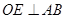 ,
,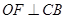 ,垂足分别是
,垂足分别是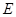 ,
,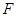 .求证
.求证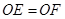 .
.
(·湖南常德)如图1,图2,分别是吊车在吊一物品时的实物图与示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为80°,吊臂AC与地面成70°角,求吊车的吊臂顶端A点距地面的高度是多少米?(精确到0.1米)?
(参考数据:sin10°=cos80°=0.17,cos10°=sin80°=0.98,sin20°=cos70°=0.34,tan70°=2.75,sin70°=0.94)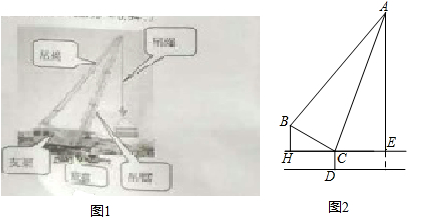
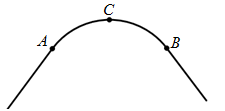
(·湖北孝感) 如图,一条公路的转弯处是一段圆弧(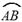 ).
).
(1)用直尺和圆规作出 所在圆的圆心
所在圆的圆心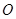 ;(要求保留作图痕迹,不写作法)
;(要求保留作图痕迹,不写作法)
(2)若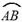 的中点
的中点 到弦
到弦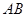 的距离为
的距离为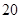 m,
m,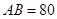 m,求
m,求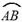 所在圆的半径.
所在圆的半径.