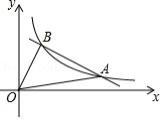
如图，直线 与反比例函数 的图象交于 ， 两点，已知点 的坐标为 ， 的面积为8．
（1）填空：反比例函数的关系式为 ；
（2）求直线 的函数关系式；
（3）动点 在 轴上运动，当线段 与 之差最大时，求点 的坐标．
探索：（1）如果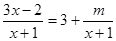
，则m=；
如果
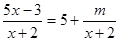，则m=；
（2）总结：如果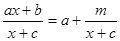
（其中a、b、c为常数），则m=；
（2）应用：利用上述结论解决：若代数式
的值为整数，求满足条件的整数x的值．
已知反比例函数y=
与一次函数y=mx+b的图象交于P(－2，1)和Q（1，n）两点．
（1）求k、n的值；
（2）求一次函数y=mx+b的解析式；
（3）求△POQ的面积．
比邻而居的蜗牛神和蚂蚁王相约，第二天上午8时结伴出发，到相距16米的银杏树下参加探讨环境保护问题的微型动物首脑会议．蜗牛神想到“笨鸟先飞”的古训，于是给蚂蚁王留下一纸便条后提前2小时独自先行，蚂蚁王按既定时间出发，结果它们同时到达．已知蚂蚁王的速度是蜗牛神的4倍，求它们各自的速度。
先化简代数式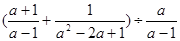
，然后选取一个你认为合适的
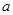值代入求值。
当x取何值时，代数式
与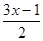
的值的差大于4？