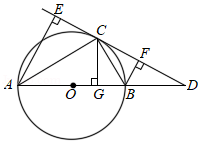
如图,在 中, 为直径,点 为圆上一点,延长 到点 ,使 ,且 .
(1)求证: 是 的切线.
(2)分别过 、 两点作直线 的垂线,垂足分别为 、 两点,过 点作 的垂线,垂足为点 .求证: .
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD于点D.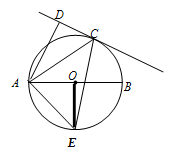
(1)求证:AC平分∠DAB;
(2)若点E为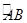 的中点,AD=
的中点,AD=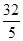 ,AC=8,求AB和AE的长.
,AC=8,求AB和AE的长.
如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为时,四边形AMDN是矩形;
②当AM的值为时,四边形AMDN是菱形。
去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
请根据图表中提供的信息解答下列问题:
(1)填空:m=,n=,扇形统计图中E组所占的百分比为;
(2)若该市人口约有75万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?
如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)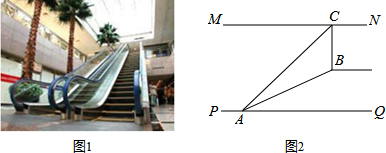
已知关于x的一元二次方程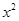 +2x+2k-2=0有两个不相等的实数根.
+2x+2k-2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若k为正整数,求该方程的根.