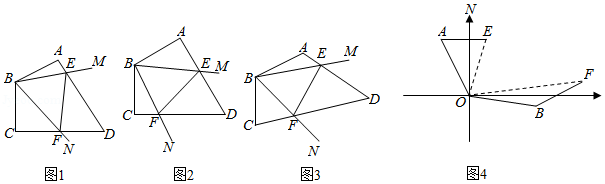
问题背景：如图1，在四边形ABCD中，∠BAD90°，∠BC-优题课

问题背景：如图1，在四边形 $ABCD$ 中， $∠ BAD = 90 °$ ， $∠ BCD = 90 °$ ， $BA = BC$ ， $∠ ABC = 120 °$ ， $∠ MBN = 60 °$ ， $∠ MBN$ 绕 $B$ 点旋转，它的两边分别交 $AD$ 、 $DC$ 于 $E$ 、 $F$ ．探究图中线段 $AE$ ， $CF$ ， $EF$ 之间的数量关系．

小李同学探究此问题的方法是：延长 $FC$ 到 $G$ ，使 $CG = AE$ ，连接 $BG$ ，先证明 $ΔBCG ≅ ΔBAE$ ，再证明 $ΔBFG ≅ ΔBFE$ ，可得出结论，他的结论就是　　；

探究延伸1：如图2，在四边形 $ABCD$ 中， $∠ BAD = 90 °$ ， $∠ BCD = 90 °$ ， $BA = BC$ ， $∠ ABC = 2 ∠ MBN$ ， $∠ MBN$ 绕 $B$ 点旋转．它的两边分别交 $AD$ 、 $DC$ 于 $E$ 、 $F$ ，上述结论是否仍然成立？请直接写出结论（直接写出"成立"或者"不成立" $)$ ，不要说明理由；

探究延伸2：如图3，在四边形 $ABCD$ 中， $BA = BC$ ， $∠ BAD + ∠ BCD = 180 °$ ， $∠ ABC = 2 ∠ MBN$ ， $∠ MBN$ 绕 $B$ 点旋转．它的两边分别交 $AD$ 、 $DC$ 于 $E$ 、 $F$ ．上述结论是否仍然成立？并说明理由；

实际应用：如图4，在某次军事演习中，舰艇甲在指挥中心 $(O$ 处）北偏西 $30 °$ 的 $A$ 处．舰艇乙在指挥中心南偏东 $70 °$ 的 $B$ 处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以75海里 $/$ 小时的速度前进，同时舰艇乙沿北偏东 $50 °$ 的方向以100海里 $/$ 小时的速度前进，1.2小时后，指挥中心观测到甲、乙两舰艇分别到达 $E$ 、 $F$ 处．且指挥中心观测两舰艇视线之间的夹角为 $70 °$ ．试求此时两舰艇之间的距离．

科目数学题型解答题难度中等

知识点：几何变换综合题全等三角形的判定与性质四边形综合题