【了解概念】
有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.

【理解运用】
(1)如图①,对余四边形 中, , , ,连接 .若 ,求 的值;
(2)如图②,凸四边形 中, , ,当 时,判断四边形 是否为对余四边形.证明你的结论;
【拓展提升】
(3)在平面直角坐标系中,点 , , ,四边形 是对余四边形,点 在对余线 上,且位于 内部, .设 ,点 的纵坐标为 ,请直接写出 关于 的函数解析式.
某超市销售有甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元。
(1)若该起市同时一次购进甲、两种商品共80件,恰好用去1600元,求能购进甲乙两种商品各多少件?
(2)该超市为使甲、乙两种商品共80件的总利润(利润=售价-进价)不少于600元,但又不超过610元,请你帮助该超市设计相应的进货方案。
如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D、E,∠AFD=158°.求:
(1)∠C的度数;
(2)∠EDF的度数。
一次知识竞赛中,一共有25道题,答对一题得10分,答错(或不答)一题扣5分.设小明同学在这次竞赛中答对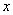 道题.
道题.
(1)根据所给条件,完成下表: 
(2)若小明同学的竞赛成绩超过100分,则他至少答对几道题?
已知:关于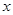 、
、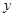 的方程组
的方程组 的解是正数,且
的解是正数,且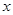 <
<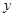 ,求
,求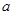 的范围。
的范围。
已知一个多边形的每个内角都比相邻外角的3倍还多20°,求这个多边形的内角和。