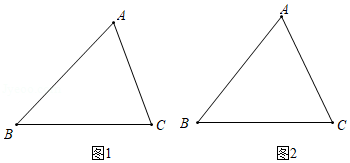
如图,已知 是锐角三角形 .
(1)请在图1中用无刻度的直尺和圆规作图:作直线 ,使 上的各点到 、 两点的距离相等;设直线 与 、 分别交于点 、 ,作一个圆,使得圆心 在线段 上,且与边 、 相切;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若 , ,则 的半径为 .
如图,将矩形ABCD中的△AOB沿着BC的方向平移线段AD长的距离.
(1)画出△AOB平移后的图形.
(2)设(1)中O点平移后的对应点为E,试判断四边形CODE的形状,并说明理由.
(3)当四边形ABCD是什么四边形时,(2)中的四边形CODE是正方形?并说明你的理由.
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,有下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF.
其中正确结论的序号是(把你认为正确的都填上).
如图,在△ABC中,AD平分∠BAC,DE∥AC交AB于点E,M是AD的中点,延长EM交AC于F.
求证:AD垂直平分线段EF.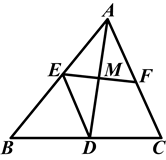
如图,在△ABC中,∠BAC=90°,AH⊥BC于H,∠ABC的平分线交AC于D,交AH于E,DF⊥BC于F.求证:四边形AEFD是菱形.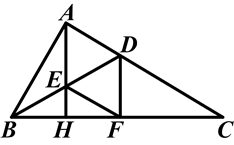
如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=10.
(1)求∠ABC的度数;
(2)求对角线AC的长度;
(3)求菱形ABCD的面积.