某工艺品厂设计了一款每件成本为11元的工艺品投放市场进行试销,经过市场调查,得出每天销售量 (件 是每件售价 (元 为正整数)的一次函数,其部分对应数据如下表所示:
每件售价 (元 |
|
15 |
16 |
17 |
18 |
|
每天销售量 (件 |
|
150 |
140 |
130 |
120 |
|
(1)求 关于 的函数解析式;
(2)若用 (元 表示工艺品厂试销该工艺品每天获得的利润,试求 关于 的函数解析式;
(3)该工艺品每件售价为多少元时,工艺品厂试销该工艺品每天获得的利润最大,最大利润是多少元?
用棋子摆出下列一组图形:
(1)、填写下表:
| 图形编号 |
1 |
2 |
3 |
4 |
5 |
6 |
| 图中棋子数 |
5 |
8 |
11 |
14 |
(2)、照这样的方式摆下去,写出摆第 个图形所需棋子的枚数;
个图形所需棋子的枚数;
(3)、其中某一图形可能共有2011枚棋子吗?若不可能,请说明理由;若可能,请你求出是第几个图形
(1) 已知x=-3是关于x的方程2k-x-k(x+4)=5的解,求k的值.
(2)在(1)的条件下,已知线段AB=12cm,点C是直线AB上一点,且AC:BC=1:k,若点D是AC的中点,求线段CD的长.
先化简,后求值
3 b-〔2a
b-〔2a -2(ab-
-2(ab-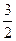
 b)+ab〕+3a
b)+ab〕+3a ,其中a=3,b=
,其中a=3,b= .
.
解下列方程:
(1)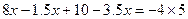 ;
;
(2)
阅读理解:
对于二次三项式 可以直接用公式法分解为
可以直接用公式法分解为 的形式,但对于二次三项式
的形式,但对于二次三项式 ,就不能直接用公式法了,我们可以在二次三项式
,就不能直接用公式法了,我们可以在二次三项式 中先加上一项
中先加上一项 ,使其成为完全平方式,再减去
,使其成为完全平方式,再减去 这项,使整个式子的值不变.于是有
这项,使整个式子的值不变.于是有 =
= +
+ -
-
= =
= =
= .
.
像上面这样把二次三项式分解因式的方法叫做添(拆)项法.
(1)请用上述方法把x2-4x+3分解因式.
(2)多项式x2+2x+2有最小值吗?如果有,那么当它有最小值时x的值是多少?