如图,射线 和射线 相交于点 , ,且 .点 是射线 上的动点(点 不与点 和点 重合),作射线 ,并在射线 上取一点 ,使 ,连接 , .
(1)如图①,当点 在线段 上, 时,请直接写出 的度数;
(2)如图②,当点 在线段 上, 时,请写出线段 , , 之间的数量关系,并说明理由;
(3)当 , 时,请直接写出 的值.

如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于点F,且BE=CF.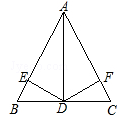
(1)求证:△BDE≌△CDF;
(2)求证:AD平分∠BAC.
在△ABC中,AB="13" cm,BC="10" cm,中线AD="12" cm.求证:△ABC是等腰三角形.
如图,等腰△ABC中,AB=AC,∠A=40°,线段AB的垂直平分线交AB于D,交AC于E,连接BE,求∠CBE的度数.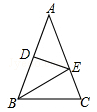
如图,C是AB的中点,AD=BE,CD=CE.求证:∠D=∠E.
利用网格线画图:如图,点A、B、C都在正方形网格的格点上.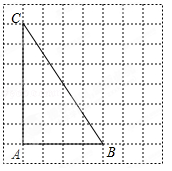
(1)在BC上找一点P,使PA=PB;
(2)在BC上找一点Q,使点Q到AB和AC的距离相等.