如图1,在平面直角坐标系中, 是坐标原点,抛物线 经过点 和点 .
(1)求抛物线的表达式;
(2)如图2,线段 绕原点 逆时针旋转 得到线段 .过点 作射线 ,点 是射线 上一点(不与点 重合),点 关于 轴的对称点为点 ,连接 , .
①直接写出 的形状为 ;
②设 的面积为 , 的面积为是 .当 时,求点 的坐标;
(3)如图3,在(2)的结论下,过点 作 ,交 的延长线于点 ,线段 绕点 逆时针旋转,旋转角为 得到线段 ,过点 作 轴,交射线 于点 , 的角平分线和 的角平分线相交于点 ,当 时,请直接写出点 的坐标为 .

如图,抛物线y=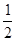 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
求抛物线的解析式及顶点D的坐标
判断△ABC的形状,证明你的结论;
点M(m,0)是x
 轴上的一个动点, 当CM+DM的值最小时,求m的值.
轴上的一个动点, 当CM+DM的值最小时,求m的值.
在数学活动课上,同学们用一根长为1米的细绳围矩形小明围出了一个面积为600㎝2的矩形,请你算一算,她围成的矩形的长和宽各是多少?
小颖想用这根细绳围成一个面积尽可能大的矩形,请你用所学过的知识帮他分析应该怎么围,并求出最大面积.
云南某蔬菜有限公司一年四季都有大量新鲜蔬菜销往全国各地,已成为我省经济发展的重要项目。近年来它的蔬菜产值不断增加,2009年蔬菜的产值是640万元,2011年产值达到1000万元。这两年的蔬菜产值增长率相同,求蔬菜产值的年平均增长率是多少?
若2012年蔬菜产值继续稳步增长(即年增长率与前两年的年增长率相同),那么请你估计2012年该公司的蔬菜产值将达到多少万元?
如图,在△ABC中, AC="BC," AB=6,O为AB的中点,且以O为圆心的半圆与AC,BC分别相切于点D,E;
AC="BC," AB=6,O为AB的中点,且以O为圆心的半圆与AC,BC分别相切于点D,E;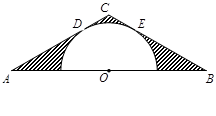
求半圆O的半径;
求图中阴影部分的面积.
先化简,再求值: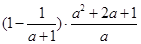 ,其中
,其中