在四边形 中, , , , ,分别以 , 为圆心,大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 ,交 于点 ,若点 是 的中点,则 的长为

| A. |
|
B. |
|
C. |
6 |
D. |
8 |
将直线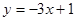 向下平移2个单位得到直线
向下平移2个单位得到直线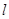 ,则直线
,则直线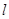 的解析式为().
的解析式为().
A.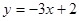 |
B.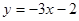 |
C.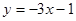 |
D.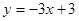 |
下列计算正确的是().
| A.a3·a4=a12 | B.(a3)4=a7 |
| C.(a2b)3=a6b3 | D.a3÷a4=a(a≠0) |
在四边形ABCD中,点O是对角线的交点,在下列条件中,能判定这个四边形为正方形的是()
| A.AC=BD,AB∥CD |
| B.AD∥BC ,∠A=∠C |
| C.OA=OB=OC=OD, AC⊥BD |
| D.OA=OC, OB=OD,AB=BC |
如图,在正方形ABCD的对角线BD是菱形BEFD的一边,菱形BEFD的对角线交正方形ABCD的一边CD于点P,∠FPC的度数是()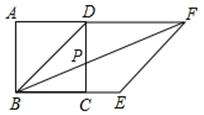
| A.135° | B.120° | C.112.5° | D.67.5° |
某销售公司有营销人员15人,销售部为了制定某种商品的月销售量定,统计了这15人某月的销售量,如下表所示:
| 每人销售件数 |
1800 |
510 |
250 |
210 |
150 |
120 |
| 人数 |
1 |
1 |
3 |
5 |
3 |
2 |
那么这15位销售人员该月销售量的平均数、众数、中位数分别是()
A.320,210,230 B.320,210,210
C.206,210,210 D.206,210,230