学校朗诵比赛,共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉一个最高分、一个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数据特征是
| A. |
平均数 |
B. |
中位数 |
C. |
众数 |
D. |
方差 |
若方程组 的解为
的解为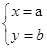 ,则一次函数y=
,则一次函数y= 与y=
与y= 交点坐标()
交点坐标()
| A.(b,a) |
| B.(a,a) |
| C.(a,b) |
| D.(b,b) |
如图,观察图象,判断下列说法错误的是()
A.方程组 的解是 的解是 |
B.不等式﹣ x+ x+ ≤2x﹣1的解集是x≥1 ≤2x﹣1的解集是x≥1 |
C.不等式﹣ x+ x+ >2x﹣1的解集是x>1 >2x﹣1的解集是x>1 |
D.方程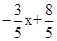 =2x﹣1的解是x=1 =2x﹣1的解是x=1 |
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组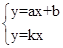 的解是()
的解是()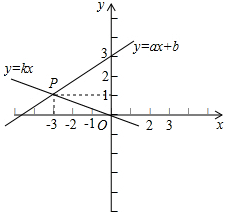
A. |
B.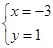 |
C. |
D. |
下列图象中,以方程﹣2x+y﹣2=0的解为坐标的点组成的图象是()
A.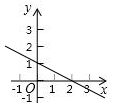 |
B. |
C. |
D. |
某校九年级(2)班40名同学这“希望工程”捐款,共捐款100元,捐款情况如下表:
| 捐款(元) |
1 |
2 |
3 |
4 |
| 人数 |
6 |
 |
7 |
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚,若设捐款2元的有x名同学,捐款3元的有y名同学,假设(x,y)是两个一次函数图象的交点,则这两个一次函数解析式分别是()
A.y=27﹣x与y=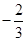 x+22
x+22
B.y=27﹣x与y=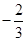 x+
x+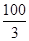
C.y=27﹣x与y=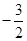 x+33
x+33
D.y=27﹣x与y=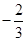 x+33
x+33