如图, CB= CA,∠ ACB=90°,点 D在边 BC上(与 B、 C不重合),四边形 ADEF为正方形,过点 F作 FG⊥ CA,交 CA的延长线于点 G,连接 FB,交 DE于点 Q,给出以下结论:
① AC= FG;② S △ FAB: S 四边形 CBFG=1:2;③∠ ABC=∠ ABF;④ AD 2= FQ• AC,
其中正确的结论的个数是( )

| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
-2的相反数是()
| A.-2 | B.2 | C.±2 | D.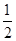 |
如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出()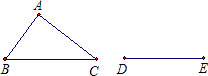
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,正六边形ABCDEF关于直线l的轴对称图形是六边形A/B/C/D/E/F/.下列判断错误的是().
| A.AB=A/B/ | B.BC//B/C/ | C.直线l⊥BB/ | D.∠A/=120° |
如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )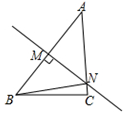
| A.1cm | B.2cm | C.3cm | D.4cm |
如图,已知AB∥CF,E为DF的中点,若AB=9cm,CF=4cm,则BD等于()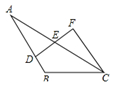
| A.2cm | B.3cm | C.4cm | D.5cm |