如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上.
(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知 ,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
,且菱形ABCD的面积是20,求矩形EFGH的长与宽.

为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图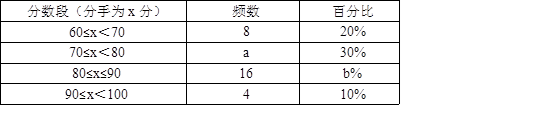
请根据图表提供的信息,解答下列问题:
(1)表中的a=,b=;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为.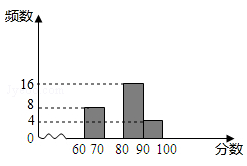
先化简,再求值: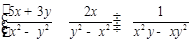 ,其中
,其中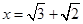 ,
,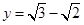 .
.
如图,在矩形ABCD中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求OE的长及经过O,D,C三点抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.
甲经销商库存有1200套A品牌服装,每套进价400元,每套售价500元,一年内可卖完,现市场流行B品牌服装,每套进价300元,每套售价600元,但一年内只允许经销商一次性订购B品牌服装,一年内B品牌服装销售无积压,因甲经销商无流动资金可用,只有低价转让A品牌服装,用转让来的资金购进B品牌服装,并销售,经与乙经销商协商,甲、乙双方达成转让协议,转让价格y(元/套)与转让数量x(套)之间的函数关系式为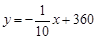 (
(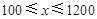 ),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).
),若甲经销商转让x套A品牌服装,一年内所获总利润为W(元).
(1)求转让后剩余的A品牌服装的销售款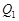 (元)与x(套)之间的函数关系式;
(元)与x(套)之间的函数关系式;
(2)求B品牌服装的销售款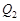 (元)与x(套)之间的函数关系式;
(元)与x(套)之间的函数关系式;
(3)求W(元)与x(套)之间的函数关系式,并求W的最大值.
已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.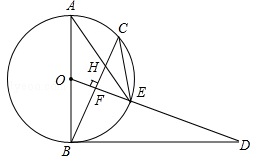
(1)求证:BD是⊙O的切线;
(2)求证: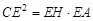 ;
;
(3)若⊙O的半径为5,sinA=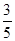 ,求BH的长.
,求BH的长.