已知反比例函数 与一次函数y=x+2的图象交于点A(﹣3,m)
(1)求反比例函数的解析式;
(2)如果点M的横、纵坐标都是不大于3的正整数,求点M在反比例函数图象上的概率.
2009年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2009~2011)》,某市政府决定2009年投入6000万元用于改善医疗卫生服务,比2008年增加了1250万元.投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2009年投入“需方”的资金将比2008年提高30%,投入“供方”的资金将比2008年提高20%.
(1)该市政府2008年投入改善医疗卫生服务的资金是多少万元?
(2)该市政府2009年投入“需方”和“供方”的资金是多少万元?
(3)该市政府预计2011年将有7260万元投入改善医疗卫生服务,若从2009~2011年每年的资金投入按相同的增长率递增,求2009~2011年的年增长率.
在△ABC中,∠B=90°,AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/s的速度作直线运动。已知点P沿射线AB运动,点Q沿边BC的延长线运动,设点P运动时间为 (s),△PCQ的面积为
(s),△PCQ的面积为 。当P运动到几秒时
。当P运动到几秒时 ?
?
阅读下面的例题:
解方程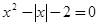
解:(1)当x≥0时,原方程化为x2–x–2=0,解得:x1=2,x2=-1(不合题意,舍去)
(2)当x<0时,原方程化为x2 + x–2=0,解得:x1=1(不合题意,舍去),x2=-2
∴原方程的根是x1="2," x2=-2;
(3)请参照例题解方程 .
.
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
在同一条件下,对同一型号的汽车进行耗油1升所行驶路程的实验,将收集到的数据作为一个样本进行分析,绘制出部分频数分布直方图和部分扇形统计图.如下图所示(路程单位:km)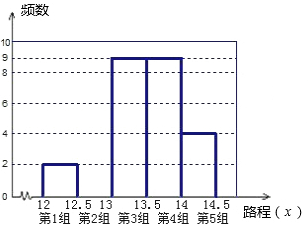
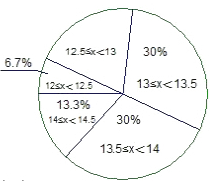
结合统计图完成下列问题:
(1)扇形统计图中,表示12.5≤x<13部分的百分数是;
(2)请把频数分布直方图补充完整,这个样本数据的中位数落在第组;
(3)哪一个图能更好地说明一半以上的汽车行驶的路程在13≤x<14之间?哪一个图能更好地说明行驶路程在12.5≤x<13的汽车多于在14≤x<14.5的汽车?