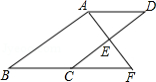
如图, O为坐标原点,点 B在 x轴上,四边形 OACB为平行四边形,cos∠ AOB= ,反比例函数 y= 在第一象限内的图象经过点 A,与 BC交于点 F.
(1)若 OA=5, OB=6,求反比例函数解析式及 C点的坐标;
(2)若点 F为 BC的中点,且△ AOF的面积为6,求 OA的长.

如图,在 中, , 是 边上一点,以 为直径的 经过 的中点 ,交 的延长线于点 ,连接 .
(1)求证: .
(2)若 , ,求 的长.

如图,在方格纸中,点 , , 都在格点上.请按要求画出以 为边的格点四边形,使 在四边形内部(不包括边界上),且 到四边形的两个顶点的距离相等.
(1)在图甲中画出一个 .
(2)在图乙中画出一个四边形 ,使 ,且 .(注:图甲、乙在答题纸上)

如图, 是 的边 的中点,延长 交 的延长线于点 .
(1)求证: .
(2)若 , , ,求 的长.
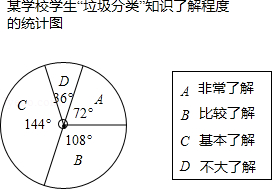
为了解学生对“垃圾分类”知识的了解程度,某学校对本校学生进行抽样调查,并绘制统计图,其中统计图中没有标注相应人数的百分比.请根据统计图回答下列问题:
(1)求“非常了解”的人数的百分比.
(2)已知该校共有1200名学生,请估计对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有多少人?
【操作发现】在计算器上输入一个正数,不断地按“ ”键求算术平方根,运算结果越来越接近1或都等于1.
【提出问题】输入一个实数,不断地进行“乘常数 ,再加上常数 ”的运算,有什么规律?
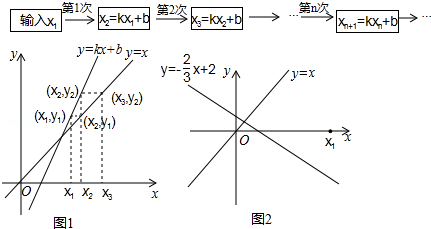
【分析问题】我们可用框图表示这种运算过程(如图 .
也可用图象描述:如图1,在 轴上表示出 ,先在直线 上确定点 , ,再在直线 上确定纵坐标为 的点 , ,然后在 轴上确定对应的数 , ,以此类推.
【解决问题】研究输入实数 时,随着运算次数 的不断增加,运算结果 ,怎样变化.
(1)若 , ,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;
(2)若 ,又得到什么结论?请说明理由;
(3)①若 , ,已在 轴上表示出 (如图2所示),请在 轴上表示 , , ,并写出研究结论;
②若输入实数 时,运算结果 互不相等,且越来越接近常数 ,直接写出 的取值范围及 的值(用含 , 的代数式表示)