在我市十个全覆盖工作的推动下，某乡镇准备在相距3千米的 A、 B两个工厂间修一条笔直的公路，在工厂 A北偏东60°方向、工厂北偏西45°方向有一点 P，以 P点为圆心，1.2千米为半径的区域是一个村庄，问修筑公路时，这个村庄是否有居民需要搬迁？（参考数据： ， ）
已知：抛物线
经过点P（﹣1，﹣2b）（b、c为常量）．
（1）求b+c的值；
（2）证明：无论b、c取何值，抛物线与x轴都有两个交点．
已知一个口袋中装有7个只有颜色不同的球，其中3个白球，4个黑球．
（1）求从中随机抽取出一个黑球的概率是多少？
（2）若往口袋中再放入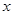
个白球和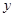
个黑球，从口袋中随机取出一个白球的概率是
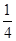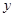，求与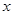之间的函数关系式．
如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，弧AE=弧 AB，BE分别交AD、AC于点F、G．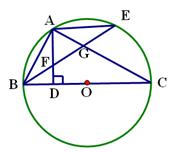
（1）判断△FAG的形状，并说明理由；
（2）若点E和点A在BC的两侧，BE、AC的延长线交于点G，AD的延长线交BE于点F，其余条件不变，（1）中的结论还成立吗？请说明理由．
已知关于
的一元二次方程
有两个实数根．
（1）求
的取值范围；
（2）设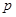
是方程的一个实数根，且满足
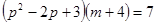，求的值．
解方程：（1）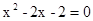
；
（2）
．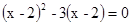