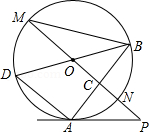
如图, PA为⊙ O的切线, A为切点,直线 PO交⊙ O于点 M、 N,过点 A作 PO的垂线 AB,垂足为 C,交⊙ O于点 B,延长 BO与⊙ O交于点 D,连接 AD、 BM.
(1)等式 OD 2= OC• OP成立吗?若成立,请加以证明;若不成立,请说明理由.
(2)若 AD=6,tan∠ M= ,求sin∠ D的值.
如图,要测量河两岸相对的两点 ,
, 的距离,可以在
的距离,可以在 的垂线
的垂线 上取两点
上取两点 ,使
,使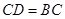 ,再定出
,再定出 的垂线
的垂线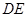 ,使
,使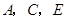 在一条直线上,这时测得的
在一条直线上,这时测得的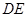 的长就是
的长就是 的长,为什么?
的长,为什么?
如图,给出五个等量关系:① 、②
、② 、③
、③ 、④
、④ 、⑤
、⑤ .
.
请你以其中两个为条件,另三个中的一个为结论,推出一个正确的命题(只需写出一种情况),并加以证明.
如图, 相交于点
相交于点 ,你能找出两对全等的三角形吗?你能说明其中的道理吗?
,你能找出两对全等的三角形吗?你能说明其中的道理吗?
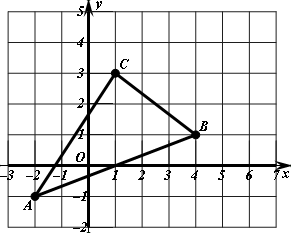
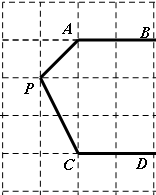
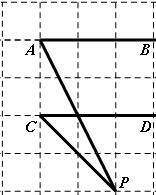
如图,在边长为 个单位长度的小正方形组成的网格中,已知
个单位长度的小正方形组成的网格中,已知 ,分别探讨下面三个图形中
,分别探讨下面三个图形中 与
与 、
、 的关系,请任选一个加以说明.(
的关系,请任选一个加以说明.( 分)
分)
( )(
)( )(
)( )
)
如图, 在平面直角坐标系中.
在平面直角坐标系中.
( )
) 点坐标是,
点坐标是, 点坐标是,
点坐标是, 点坐标是;(
点坐标是;( 分)
分)
( )把
)把 先向右平移
先向右平移 个单位,再向上平移
个单位,再向上平移 个单位,画出平移后的
个单位,画出平移后的 .(
.( 分)
分)
( )求
)求 的面积
的面积 .(
.(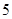 分)
分)