如图1,在△ ABC中,设∠ A、∠ B、∠ C的对边分别为 a, b, c,过点 A作 AD⊥ BC,垂足为 D,会有sin∠ C= ,则
S △ ABC= BC× AD= × BC× ACsin∠ C= absin∠ C,
即 S △ ABC= absin∠ C
同理 S △ ABC= bcsin∠ A
S △ ABC= acsin∠ B
通过推理还可以得到另一个表达三角形边角关系的定理﹣余弦定理:
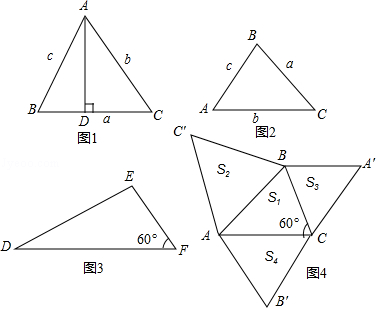
如图2,在△ ABC中,若∠ A、∠ B、∠ C的对边分别为 a, b, c,则
a 2= b 2+ c 2﹣2 bccos∠ A
b 2= a 2+ c 2﹣2 accos∠ B
c 2= a 2+ b 2﹣2 abcos∠ C
用上面的三角形面积公式和余弦定理解决问题:
(1)如图3,在△ DEF中,∠ F=60°,∠ D、∠ E的对边分别是3和8.求 S △ DEF和 DE 2.
解: S △ DEF= 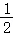 EF× DFsin∠ F= ;
EF× DFsin∠ F= ;
DE 2= EF 2+ DF 2﹣2 EF× DFcos∠ F= .
(2)如图4,在△ ABC中,已知 AC> BC,∠ C=60°,△ ABC'、△ BCA'、△ ACB'分别是以 AB、 BC、 AC为边长的等边三角形,设△ ABC、△ ABC'、△ BCA'、△ ACB'的面积分别为 S 1、 S 2、 S 3、 S 4,求证: S 1+ S 2= S 3+ S 4.
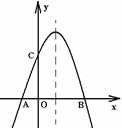
如图,抛物线的对称轴是直线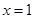 ,它与
,它与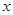 轴交于
轴交于 ,
,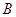 两点,与
两点,与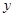 轴交于
轴交于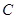 点,点
点,点 ,
,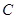 的坐标分别是
的坐标分别是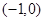 ,
,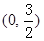 .
.
(1) 求此抛物线对应的函数解析式;
(2) 若点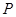 是抛物线上位于
是抛物线上位于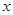 轴上方的一个动点,求△ABP面积的最大值.
轴上方的一个动点,求△ABP面积的最大值.
如图,△ABC内接于半圆,AB为直径,设D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.
求证:FD=FG.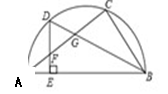
如图1,抛物线y= -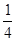 x2+
x2+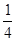 x+3与x轴交于A.C两点,与y轴交于B点,与直线y=kx+b交于A.D两点.
x+3与x轴交于A.C两点,与y轴交于B点,与直线y=kx+b交于A.D两点.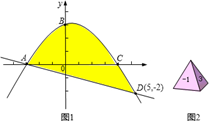
(1)直接写出A、C两点坐标和直线AD的解析式;
(2)如图2,质地均匀的正四面体骰子的各个面上依次标有数字-1.1.3.4.随机抛掷这枚骰子两次,把第一次着地一面的数字m记做P点的横坐标,第二次着地一面的数字n记做P点的纵坐标.则点P(m,n)落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
已知抛物线的顶点(-1,-2)且图象经过(1,6),求此抛物线解析式.
(1)求该二次函数的解析式;
(2)当y>0时,x的取值范围.
如图,破残的圆形轮片上,弦AB的垂直平分线交AB于C,交弦AB于D.
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)若AB=24cm,CD=8cm,求(1)中所作圆的半径.