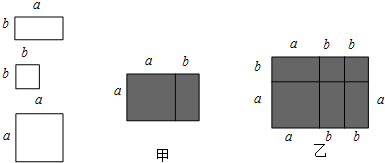已知抛物线 y= a( x﹣1) 2+3( a≠0)与 y轴交于点 A(0,2),顶点为 B,且对称轴 l 1与 x轴交于点 M
(1)求 a的值,并写出点 B的坐标;
(2)有一个动点 P从原点 O出发,沿 x轴正方向以每秒2个单位的速度运动,设运动时间为 t秒,求 t为何值时 PA+ PB最短;
(3)将此抛物线向右平移所得新的抛物线与原抛物线交于点 C,且新抛物线的对称轴 l 2与 x轴交于点 N,过点 C作 DE∥ x轴,分别交 l 1, l 2于点 D、 E,若四边形 MDEN是正方形,求平移后抛物线的解析式.

小强和小勇想利用课本上学过的知识来进行台球比赛:小强把白球放在如图所示的位置,想通过击打白球撞击黑球,使黑球撞AC边后反弹进F洞;想想看,小强这样打,黑球能进F洞吗?请用画图的方法验证你的判断,并说出理由.
计算:(4a﹣3b)•(a﹣2b)
若(x﹣1)(x2+mx+n)=x3﹣6x2+11x﹣6,求m,n的值.
先化简,再求值:5(3x2y﹣xy2)﹣4(﹣xy2+3x2y),其中x=﹣2,y=3.
如图,有多个长方形和正方形的卡片,图甲是选取了2块不同的卡片,拼成的一个图形,借助图中阴影部分面积的不同表示可以用来验证等式a(a+b)=a2+ab成立.
(1)根据图乙,利用面积的不同表示方法,写出一个代数恒等式;
(2)试写出一个与(1)中代数恒等式类似的等式,并用上述拼图的方法说明它的正确性.