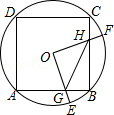
如图,边长为4的正方形ABCD内接于圆O,点E是 上的一动点(不与A、B重合),点F是 上的一点,连接OE、OF,分别与AB、BC交于点G,H,且 ,有以下结论:
① ;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为 .
其中正确的是 (把你认为正确结论的序号都填上).
若关于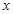 的方程
的方程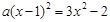 是一元二次方程,则
是一元二次方程,则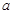 的值是 .
的值是 .
24点游戏是一种使用扑克牌来进行的益智类游戏,游戏内容是:从一副扑克牌中抽去大小王剩下52张,任意抽取4张牌,把牌面上的数运用你所学过的运算得出24.每张牌都必须使用一次,但不能重复使用.
(1)在玩“24点”游戏时,小明抽到以下4张牌:



请你帮他写出运算结果为24的算式:(写出2个)
_______________________; _______________________;
(2)如果  .
. 表示正,
表示正, .
. 表示负,请你用(1)中的4张牌表示的数写出运算结果为24的算式(写出2个):
表示负,请你用(1)中的4张牌表示的数写出运算结果为24的算式(写出2个):
__________________________; __________________________;
(3)如果小明抽到以下4张牌:



请你用这4张牌表示的数写出运算结果为24的一个算式:
__________________________.
假设一家旅馆一共有30个房间,分别编以1-30号三十个号码,现在要在每个房间的钥匙上刻上数字,要求所刻数字必须使服务员很容易辨认是哪一个房间的钥匙,而使外人不容易猜到,现在有一种编码方法是:在每把钥匙上刻上两个数字,左边的一个数字是这把钥匙原来的房间号除以5所得的余数,而右边的一个数字是这把钥匙原来的房间号码除以7所得的余数,那么刻的数是36的钥匙所对应的原来房间应该是___________号.
若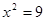 ,则x=________,
,则x=________, 则x=________.
则x=________.
已知实数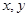 满足
满足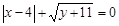 ,则代数式
,则代数式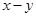 =_____________.
=_____________.