如图，直线 y＝﹣ x+2与反比例函数 y＝ （ k≠0）的图象交于 A（ a，3）， B（3， b）两点，过点 A作 AC⊥ x轴于点 C，过点 B作 BD⊥ x轴于点 D．
（1）求 a， b的值及反比例函数的解析式；
（2）若点 P在直线 y＝﹣ x+2上，且 S △ ACP＝ S △ BDP，请求出此时点 P的坐标；
（3）在 x轴正半轴上是否存在点 M，使得△ MAB为等腰三角形？若存在，请直接写出 M点的坐标；若不存在，说明理由．
如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点，
求证：（1）
；（2）
.
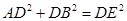将分别标有数字1，2，3 的三张卡片洗匀后，背面朝上放在桌面上.
（1）随机抽取一张，求抽到奇数的概率；
（2）随机抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字，能组成哪些两位数？恰好是32的概率是多少.
某种电脑病毒传播非常快，如果一台电脑被感染，经过两轮感染后就会有81台电脑被感染．请你用学过的知识分析，每轮感染中平均一台电脑会感染几台电脑？若病毒得不到有效控制，3轮感染后，被感染的电脑会不会超过700台？
如图，已知一次函数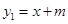
（m为常数）的图象与反比例函数
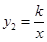（k为常数，
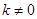）的图象相交于点 A（1，3）.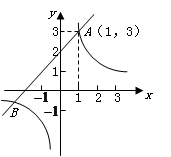
（1）求这两个函数的解析式及其图象的另一交点
的坐标；
（2）观察图象，写出使函数值
的自变量
的取值范围.
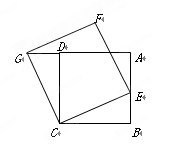
如图，已知正方形
，点
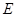是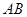
上的一点，连结
，以为一边，在的上方作正方形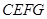
，连结
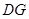．求证：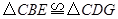
.