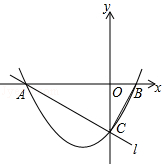
如图,在平面直角坐标系中,已知抛物线 y= x 2+ x﹣2与 x轴交于 A, B两点(点 A在点 B的左侧),与 y轴交于点 C,直线 l经过 A, C两点,连接 BC.
(1)求直线 l的解析式;
(2)若直线 x= m( m<0)与该抛物线在第三象限内交于点 E,与直线 l交于点 D,连接 OD.当 OD⊥ AC时,求线段 DE的长;
(3)取点 G(0,﹣1),连接 AG,在第一象限内的抛物线上,是否存在点 P,使∠ BAP=∠ BCO﹣∠ BAG?若存在,求出点 P的坐标;若不存在,请说明理由.
读出下列语句,并按照这些语句画出图形
(1)两条直线a、b,相交于点P.
(2)直线l经过A、B、C三点,点C在点A与点B之间.
(3)直线a经过点A、B,点P不在直线a上.
图中给出的各角中,哪些互为余角?哪些互为补角?
请你用三角板、圆规或量角器等工具,画∠POQ=60°,在它的边OP上截取OA="50" mm,OQ上截取OB="70" mm,连结AB,画∠AOB的平分线与AB交于点C,并量出AC和OC 的长.(结果精确到1 mm,不要求写作法).
下列说法中正确的是( )
| A.一条射线把一个角分成两个角,这条射线是这个角的角平分线 |
| B.点到直线的距离是指从直线外一点到这条直线的垂线的长度 |
C.若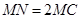 ,则点 ,则点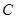 是线段 是线段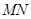 的中点 的中点 |
D.有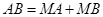 , ,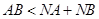 ,则点 ,则点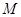 在线段 在线段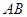 上,点 上,点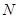 在线段 在线段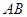 外 外 |
如图,平原上有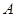 ,
,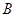 ,
,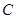 ,
,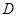 四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.
⑴不考虑其他因素,请你画图确定蓄水池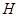 点的位置,使它与四个村庄的距离之和最小.
点的位置,使它与四个村庄的距离之和最小.
⑵计划把河中的水引入蓄水池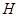 中,怎样开的渠最短?并说明根据.
中,怎样开的渠最短?并说明根据.