国家为了实现2020年全面脱贫目标，实施"精准扶贫"战略，采取异地搬迁，产业扶持等措施．使贫困户的生活条件得到改善，生活质量明显提高．某旗县为了全面了解贫困县对扶贫工作的满意度情况，进行随机抽样调查，分为四个类别： A．非常满意； B．满意； C．基本满意； D．不满意．依据调查数据绘制成图1和图2的统计图（不完整）．
根据以上信息，解答下列问题：
（1）将图1补充完整；
（2）通过分析，贫困户对扶贫工作的满意度（ A、 B、 C类视为满意）是 ；
（3）市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中，随机抽取两户进行满意度回访，求这两户贫困户恰好都是同一乡镇的概率．
当
取什么数时,
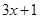与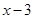
互为相反数｡
一年前明明用80元压岁钱买了债券，一年后的本息正好够买1台录音机，已知录音机每台92元，问明明买的债券年利率是百分之几？
敌我两军相距25千米，敌军以每小时5千米的速度逃跑，我军同时以每小时8千米的速度追去，并在相距1千米处发生战斗，问战斗是在开始追去几小时后发生的？
8位退休教师分别乘坐小汽车从山区赶往飞机场,可真不巧,其中一辆小汽车在距离飞机场15千米的地方出了故障,不能行驶,此时离飞机停止检票时间只剩下42分钟(停止检票后即不让乘客上飞机).这时,惟一可以利用的交通工具只剩下一辆小汽车,连同司机在内一次限乘5人,这辆小汽车的平均速度为60千米/ 时.
（1）这辆小汽车要分两批送这8人,如果第二批人在原地等待,那么这8 人都能及时到达机场吗?请说明理由.
（2）如果在小汽车送第一批人的同时,第二批人先步行; 小汽车把第一批人送到机场后立即返回接送在步行中的第二批人, 若这些人的步行速度为5千米/时,问:这8人都能及时到达机场吗?请说明理由.
某学校班主任暑假带领该班三好学生去旅游，甲旅行社说：“如果教师买全票一张，其余学生享受半价优惠；”乙旅行社说：“教师在内全部按票价的6折优惠；”若全部票价是240元.
（1）如果有10名学生，应参加哪个旅行社，并说出理由；
（2）当学生人数是多少时，两家旅行社收费一样多？