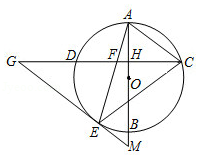
如图,△ ACE内接于⊙ O, AB是⊙ O的直径,弦 CD⊥ AB于点 H,交 AE于点 F,过点 E作 EG∥ AC,分别交 CD、 AB的延长线于点 G、 M.
(1)求证:△ ECF∽△ GCE;
(2)若tan G= , AH=3 ,求⊙ O半径.
(1)证明:不论 取什么值,直线
取什么值,直线 :y=
:y= x-
x- 都通过一个定点;
都通过一个定点;
(2)以A(0,2)、B(2,0)、O(0,0)为顶点的三角形被直线 分成两部分,分别求出当
分成两部分,分别求出当 =2和
=2和 =-
=-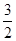 时,靠近原点O一侧的那部分面积.
时,靠近原点O一侧的那部分面积.
如图,AD=BC,AC=BD,AC、BD相交于O,求证:AB∥CD.
已知A=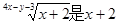 的算术平方根,B=
的算术平方根,B=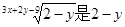 的立方根,求A+B的立方根.
的立方根,求A+B的立方根.
已知: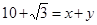 ,其中
,其中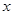 是整数,且
是整数,且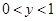 ,求
,求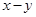 的相反数.
的相反数.
如图,在平面直角坐标系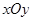 中,长方形
中,长方形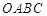 的顶点
的顶点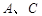 的坐标分别为
的坐标分别为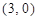 ,
,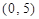 .
.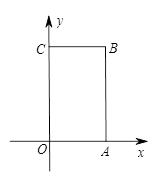
(1)直接写出点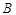 的坐标;
的坐标;
(2)若过点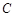 的直线
的直线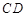 交
交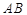 边于点
边于点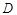 ,且把长方形
,且把长方形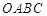 的周长分为1:3两部分,求直线
的周长分为1:3两部分,求直线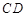 的解析式;
的解析式;
(3)设点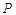 沿
沿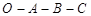 的方向运动到点
的方向运动到点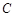 (但不与点
(但不与点 重合),求△
重合),求△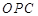 的面积
的面积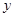 与点
与点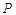 所行路程之间的函数关系式及自变量
所行路程之间的函数关系式及自变量 的取值范围.
的取值范围.