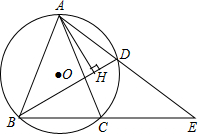
如图,△ ABC内接于⊙ O, BC=2, AB= AC,点 D为 上的动点,且cos∠ ABC= .
(1)求 AB的长度;
(2)在点 D的运动过程中,弦 AD的延长线交 BC延长线于点 E,问 AD• AE的值是否变化?若不变,请求出 AD• AE的值;若变化,请说明理由;
(3)在点 D的运动过程中,过 A点作 AH⊥ BD,求证: BH= CD+ DH.
如图,在平面直角坐标系内,点A的坐标为(0,12),经过原点的直线l,与经过点A的直线12相交于点B,点B的坐标为(9,3).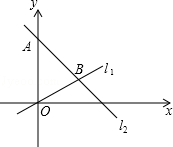
(1)求直线l1,l2的表达式;
(2)点C为直线l1上一动点,作CD∥y轴交直线l2于点D,若CD=8,求点C的坐标.
2014年世界杯足球赛在巴西举行,小李在网上预订了小组赛和淘汰赛两个阶段的球票共10张,总价为5800元.其中小组赛球票每张550元,淘汰赛球票每张700元,问小李预定了小组赛和淘汰赛的球票各多少张?
如图,在平面直角坐标系中,
(1)描出A(- 4,3)B(-1,0)C(-2,3)三点.
(2)△ABC的面积是
(3)作出△ABC关于y轴的对称图形.
(1)求直线y=2x﹣6与坐标轴的交点坐标.
(2)“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上的行驶速度不得超过70千米 /时.一辆“小汽车”在一条城市街路上直道行驶,某一时刻刚好行驶到路对面“车速检测仪A”正前方50米C处,过了6秒后,测得“小汽车”位置B与“车速检测仪A”之间的距离为130米,这辆“小汽车”超速了吗?请说明理由.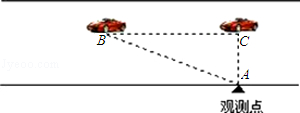
(1)计算 (1﹣ )2+
)2+ .
.
(2)解方程组