若两条抛物线的顶点相同,则称它们为"友好抛物线",抛物线 C 1: y 1=﹣2 x 2+4 x+2与 C 2: y 2=﹣ x 2+ mx+ n为"友好抛物线".
(1)求抛物线 C 2的解析式.
(2)点 A是抛物线 C 2上在第一象限的动点,过 A作 AQ⊥ x轴, Q为垂足,求 AQ+ OQ的最大值.
(3)设抛物线 C 2的顶点为 C,点 B的坐标为(﹣1,4),问在 C 2的对称轴上是否存在点 M,使线段 MB绕点 M逆时针旋转90°得到线段 MB′,且点 B′恰好落在抛物线 C 2上?若存在求出点 M的坐标,不存在说明理由.
如图,抛物线 与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).
与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).求直线AB的函数关系式;
动点P在线段OC上从原点出发以每秒一个单位的速度向C移动,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N. 设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM,BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.

如图,在平面直角坐标系中有一矩形ABCO,B点的坐标为(12,6),点C、A在坐标轴上.⊙A、⊙P的半径均为1,点P从点C开始在线段CO上以1单位/秒的速度向左运动,运动到点O处停止.与此同时,⊙A的半径每秒钟增大2个单位,当点P停止运动时,⊙A的半径也停止变化.设点P运动的时间为t秒.在0<t<12时,设△OAP的面积为s,试求s与t的函数关系式.并求出当t为何值时,s为矩形ABCO面积的
 ;
;在点P的运动过程中,是否存在某一时刻,⊙A与⊙P相切,若存在求出点P的坐标,若不存在,说明理由.

如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=4㎝,DC=6㎝,试求AD的长. 小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题。请按照小萍的思路,探究并解答下列问题:分别以AB、AC所在的直线为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点分别为点E、F,延长EB、FC相交于G点,试证明四边形AEGF是正方形;
设AD=x㎝,联系(1)的结论,试求出AD的长;

某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: .
.设李明每月获得利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
如果李明想要每月获得2000元的利润,那么销售
 单价应定为多少元?
单价应定为多少元?根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
2011年5月19日,中国首个旅游日正式启动.某校组织了八年级800名学生参加的旅游地理知识竞赛,李老师为了了解学生对旅游地理知识的掌握情况,从中随机抽取了部分学生的成绩作为样本,把成绩按优秀、良好、及格和不及格4个级别进行统计,并绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).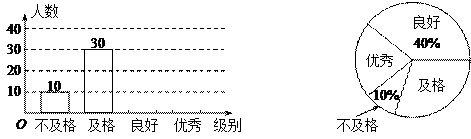
请根据以上提供的信息,解答下列问题:求被抽取部分学生的人数;
请补全条形统计图,并求出扇形统计图中表示及格的扇形的圆心角度数;
请估计八年级800名学生中达到良好和优秀的总人数.