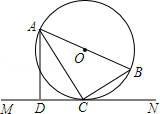
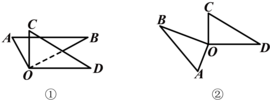如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且 .
(1)求证:直线MN是⊙O的切线;
(2)若 , ,求⊙O的半径.
(本小题满分8分)如图,已知一次函数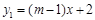 与正比例函数
与正比例函数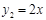 图像相交于点A
图像相交于点A 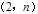 ,
,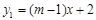 与
与 轴交于点B.
轴交于点B.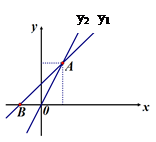
(1)求出m、n的值;
(2)求出 的面积.
的面积.
(本小题满分8分)为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶6次,命中的环数如下(单位:环):
甲:7,8,8,6,10,9乙:9,6,7,8,9,9
(1)求甲、乙两名选手的射击平均成绩分别是多少?
(2)如果你是教练,你会派哪一位选手参加比赛?请说明理由.
(本小题满分8分)如图,E、F分别为□ABCD对角线BD上的点,且BE=DF.
求证:AE=CF.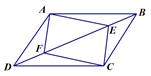
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O—C—B—A—O的路线移动(即:沿着长方形移动一周).
(1)写出点B的坐标( ).
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
如图①②,将两个相同三角板的两个直角顶点O重合在一起,如图①②放置.
(1)若∠BOC=60°,如图①求∠AOD的度数;
(2)若∠BOC=70°,如图②求∠AOD的度数;
(3)猜想∠AOD和∠BOC的关系.