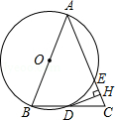
如图,在 中, ,以 为直径的 与边 , 分别交于 , 两点,过点 作 于点 .
(1)判断 与 的位置关系,并说明理由;
(2)求证: 为 的中点;
(3)若 , ,求 的长.
如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1km,BD=3km,CD=3km,现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20000元/千米,请你在CD选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用F。(本题7分)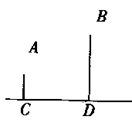
(本题13分)某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500㎏,销售单价每涨1元,月销售量就减少10㎏,针对这种水产品,请解答以下问题:
⑴当销售单价定为每千克55元时,计算销售量与月销售利润。
⑵设销售单价为每千克x元,月销售利润为y元,求y与x的关系式;
⑶当销售单价为多少时,月销售利润最大?最大利润是多少?
⑷商店想在销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为多少?
(本题8分)利用一面长45米的墙,用80m长的篱笆围成一个矩形场地。
⑴怎样才能使矩形场地面积为750㎡?
⑵能否使所围矩形场地的面积为810㎡,为什么?
(本题8分)某电脑公司2008年的各项经营收入中,经营电脑配件的收入为600万元,占全年经营总收入的40%,该公司预计2010年经营总收入要达到2160万元,且计划从2008年到2010年每年经营总收入的年增长率相同,问2009年预计经营总收入为多少万元?
(本题8分)若关于x的方程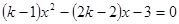 有两个相等的实数根,求实数k的值。
有两个相等的实数根,求实数k的值。