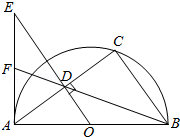
如图,已知 为半圆 的直径, 为半圆 上一点,连接 , ,过点 作 于点 ,过点 作半圆 的切线交 的延长线于点 ,连接 并延长交 于点 .
(1)求证: ;
(2)若半圆 的直径为10, ,求 的长.
如图,在∆ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.
求证:∠CBE=∠BAD.
解不等式 并写出它的所有非负整数解.
并写出它的所有非负整数解.
已知2a2+3a-6=0,水代数式3a(2a+1)-(2a+1)(2a-1)的值.
阅读理解:
学习了三角形全等的判定方法:“SAS”,“ASA”,“AAS”,“SSS”和直角三角形全等的判定方法“HL”后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”即“SSA”的情形进行研究.
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D.
初步探究:
如图1,已知AC="DF," ∠A=∠D,过C作CH⊥射线AM于点H,对△ABC 的CB边进行分类,可分为“CB<CH,CB=CH,CH<CB<CA,”三种情况进行探究.
深入探究:
第一种情况,当BC<CH时,不能构成△ABC和△DEF.
第二种情况,(1)如图2,当BC=CH时,在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D,根据,可以知道Rt△ABC≌Rt△DEF.
第三种情况,(2)当CH<BC<CA时,△ABC和△DEF不一定全等.请你用尺规在图1的两个图形中分别补全△ABC和△DEF,使△DEF和△ABC不全等(表明字母,不写作法,保留作图痕迹).
(3)从上述三种情况发现,只有当BC=CH时,才一定能使△ABC≌△DEF.除了上述三种情况外,BC边还可以满足什么条件,也一定能使△ABC≌△DEF?写出结论,并利用备用图证明.
在△ABC内侧作射线 ,自B,C分别向射线AP引垂线,垂足分别为D,E,M为BC边中点,连接MD,ME.
,自B,C分别向射线AP引垂线,垂足分别为D,E,M为BC边中点,连接MD,ME.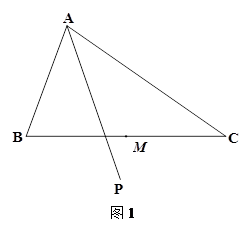

(1)依题意补全图1;
(2)求证:MD=ME;
(3)如图2,若射线AP平分∠BAC,且AC>AB,求证:MD= .
.