某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
甲 |
乙 |
丙 |
|
每辆汽车能装的数量(吨 |
4 |
2 |
3 |
每吨水果可获利润(千元) |
5 |
7 |
4 |
(1)用8辆汽车装运乙、丙两种水果共22吨到 地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到 地销售(每种水果不少于一车),假设装运甲水果的汽车为 辆,则装运乙、丙两种水果的汽车各多少辆?(结果用 表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
已知关于x的一元二次方程(x-3)(x-2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.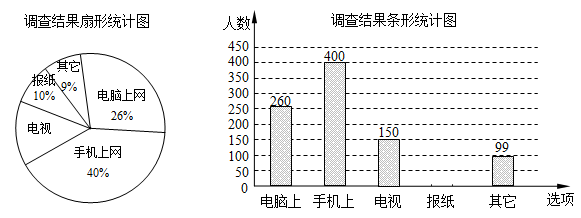
根据以上信息解答下列问题:
(1)这次接受调查的市民总人数是 ;
(2)扇形统计图中,“电视”所对应的圆心角的度数是 ;
(3)请补全条形统计图;
(4)若该市约有80万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD,PO.
(1)求证:△CDP≌△POB;
(2)填空:
① 若AB=4,则四边形AOPD的最大面积为 ;
② 连接OD,当∠PBA的度数为 时,四边形BPDO是菱形.
先化简,再求值: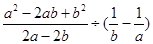 ,其中
,其中 ,
,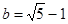 .
.
在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r.则称P′为点P关于⊙C的反称点,下图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.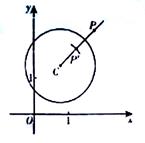
(1)当⊙O的半径为1时.
①分別判断点M(2,1),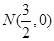 ,
, 关于⊙O的反称点是否存在?若存在,求其坐标;
关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=-x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x袖上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x袖上,半径为1,直线 与x轴、y轴分別交于点A,B.若线段AB存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分別交于点A,B.若线段AB存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.