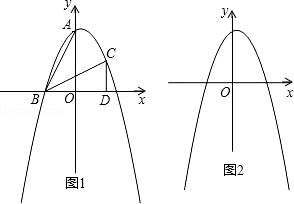
在直角坐标系 中, 、 ,将 经过旋转、平移变化后得到如图1所示的 .
(1)求经过 、 、 三点的抛物线的解析式;
(2)连接 ,点 是位于线段 上方的抛物线上一动点,若直线 将 的面积分成 两部分,求此时点 的坐标;
(3)现将 、 分别向下、向左以 的速度同时平移,求出在此运动过程中 与 重叠部分面积的最大值.
如图在ΔABC中AB=AC,∠BAC=900,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F
(1)求证:AE=CF(提示:添辅助线)
(2)是否还有其他结论,不要求证明(至少2个)
如图:点D在⊿ABC的边AB上,连接 CD,∠1=∠B,AD=4,AC=6, 求:BD的长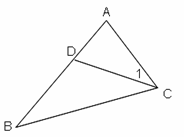
求证:在直角三角形中,如果有一个锐角等于30°,那么这个锐角所对的直角边等于斜边的一半
已知:等腰△ABC中,AB=AC=13,BC=10,求底角∠B的正弦、余弦、正切值。
如图,点E在AB上,点G在CD上,EF⊥GF于F,∠CGF=150°,∠BEF=60°,试判断AB和CD的位置关系,并说明理由.