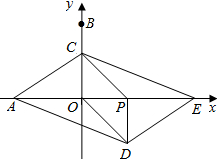
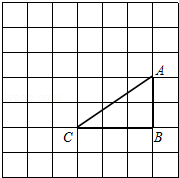
如图,在边长为1的正方形网格中, 的顶点均在格点上,点 、 的坐标分别是 、 ,把 绕点 逆时针旋转 后得到△ .
(1)画出△ ,直接写出点 、 的坐标;
(2)求在旋转过程中, 所扫过的面积.
为增强居民节约用电意识,某市对居民用电实行“阶梯收费”,具体收费标准见表:
| 一户居民一个月用电量的范围 |
电费价格(单位:元/千瓦时) |
| 不超过160千瓦时的部分 |
x |
| 超过160千瓦时的部分 |
x+0.15 |
某居民五月份用电190千瓦时,缴纳电费90元.
(1)求x和超出部分电费单价;
(2)若该户居民六月份所缴电费不低于75元且不超过84元,求该户居民六月份的用电量范围.
我州实施新课程改革后,学生的自主字习、合作交流能力有很大提高.某学校为了了解学生自主学习、合作交流的具体情况,对部分学生进行了为期半个月的跟踪调査,并将调査结果分类,A:特别好;B:好;C:一般;D:较差.现将调査结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)本次调查中,一共调査了名同学,其中C类女生有名;
(2)将下面的条形统计图补充完整;
(3)为了共同进步,学校想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男生、一位女生的概率.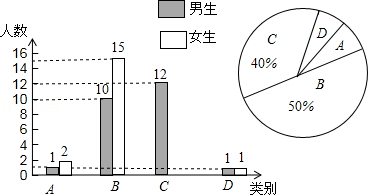
如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=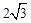 .
.
(1)求证:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)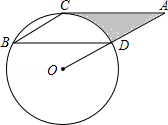
解方程: .
.
如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动。以CP,CO为邻边构造□PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为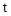 秒.
秒.
(1)当点C运动到线段OB的中点时,求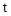 的值及点E的坐标;
的值及点E的坐标;
(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形;
(3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在第一、四象限,在运动过程中,设□PCOD的面积为S.
①当点M,N中,有一点落在四边形ADEC的边上时,求出所有满足条件的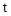 的值;
的值;
②若点M,N中恰好只有一个点落在四边形ADEC内部(不包括边界)时,直接写出S的取值范围.