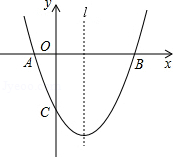
如图,已知抛物线 经过 、 、 三点,直线 是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点 是直线 上的一个动点,当点 到点 、点 的距离之和最短时,求点 的坐标;
(3)点 也是直线 上的动点,且 为等腰三角形,请直接写出所有符合条件的点 的坐标.
(1)计算: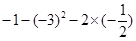 ;
;
(2)解方程: .
.
图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状围成一个正方形.
(1)图②中的阴影部分是个______________形(填长方形或正方形),它的边长为;
(2)观察图②阴影部分的面积,请你写出三个代数式(m+n)2、(m-n)2、mn之间的等量关系是.
(3)实际上有许多代数恒等式可以用图形的面积来表示.如图③,它表示了.
已知 。
。
(1)求a-b的值。
(2)求 的值。
的值。
某市出租车收费标准是:起步价10元,可乘3千米;3千米到5千米,每千米1.3元;超过5千米,每千米2.4元。
(1)若某人乘坐了 (
( )千米的路程,则他应支付的费用是多少?
)千米的路程,则他应支付的费用是多少?
(2)若某人乘坐的路程为6千米,那么他应支付的费用是多少?
合并同类项
(1)3x-y-2x+3y;
(2)3a2b+2ab2+5-3a2b-5ab2-2.