-2的相反数是【】
| A.2 | B.-2 | C.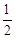 |
D.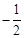 |
如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为【】
A.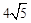 cm cm |
B.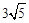 cm cm |
C.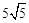 cm cm |
D.4 cm |
如图,反比例函数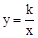 (x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为【】
(x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为【】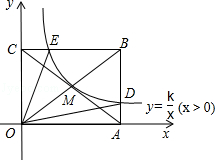
A.1 B.2 C.3 D.4
同时抛掷A、B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x、y,并以此确定点P(x,y),那么点P落在抛物线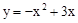 上的概率为【】
上的概率为【】
A.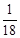 B.
B.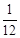 C.
C.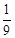 D.
D.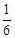
若抛物线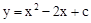 与y轴的交点为(0,﹣3),则下列说法不正确的是【】
与y轴的交点为(0,﹣3),则下列说法不正确的是【】
| A.抛物线开口向上 |
| B.抛物线的对称轴是x=1 |
| C.当x=1时,y的最大值为﹣4 |
| D.抛物线与x轴的交点为(-1,0),(3,0) |