为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
|
|
七年级 |
0 |
1 |
0 |
|
7 |
1 |
八年级 |
1 |
0 |
0 |
7 |
|
2 |
分析数据:
平均数 |
众数 |
中位数 |
|
七年级 |
78 |
75 |
|
八年级 |
78 |
|
80.5 |
应用数据:
(1)由上表填空: , , , .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
会堂里竖直挂一条幅AB,如图,小刚从与B成水平的C点观察,视角∠C=30°,当他沿CB方向前进2米到达到D时,视角∠ADB=45°,求条幅AB的长度。
已知反比例函数y= 的图象与二次函数y=ax2+x-1的图象相交于点(2,2)
的图象与二次函数y=ax2+x-1的图象相交于点(2,2)
(1)求a和k的值;
(2)反比例函数的图象是否经过二次函数图象的顶点,为什么?
2010年亚运会在中国广州举办, 期间在市政府广场进行了热气球飞行表演.如图,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)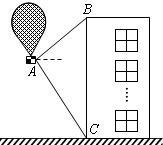
(参考数据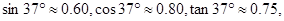
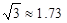 )
)
如图,A、D、B、C是⊙O上的四点,∠ADC=∠CDB=60°,判断△ABC的形状并证明你的结论。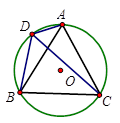
已知二次函数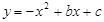 的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)。
的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)。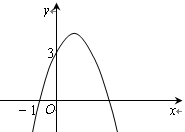
(1)求出b,c的值,并写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围。