某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现唱歌类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从 开始, 之前演出结束,问参与的小品类节目最多能有多少个?
(本题8分)某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务有甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题: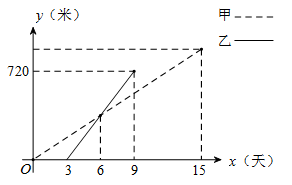
(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成?
(本题8分)某水果销售点用1000元购进甲、乙两种新出产的水果共140千克,这两种水果的进价、售价如表所示:
| 进价(元/千克) |
售价(元/千克) |
|
| 甲种 |
5 |
8 |
| 乙种 |
9 |
13 |
(1)这两种水果各购进多少千克?
(2)若该水果店按售价销售完这批水果,获得的利润是多少元?
(本题8分)某学校举行“社会主义核心价值观”知识比赛活动,全体学生都参加比赛,学校对参赛学生均给与表彰,并设置一、二、三等奖和纪念奖共四个奖项,赛后将获奖情况绘制成如下所示的两幅不完整的统计图,请根据图中所给的信息,解答下列问题:
(1)该校共有名学生;
(2)在图1中,“三等奖”随对应扇形的圆心角度数是;
(3)将图2补充完整;
(4)从该校参加本次比赛活动的学生中随机抽查一名.求抽到获得一等奖的学生的概率.
(本题8分)如图,在△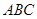 中,
中,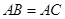 ,点
,点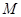 在
在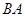 的延长线上.
的延长线上.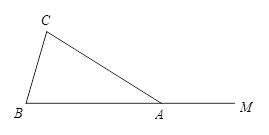
(1)按下列要求作图,并在图中标明相应的字母.
①作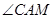 的平分线
的平分线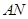 ;
;
②作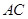 的中点
的中点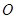 ,连接
,连接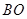 ,并延长
,并延长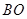 交
交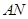 于点
于点 ,连接
,连接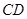 .
.
(2)在(1)的条件下,判断四边形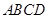 的形状.并证明你的结论.
的形状.并证明你的结论.
(本题6分)先化简,再求值: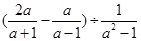 ,其中
,其中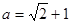 .
.