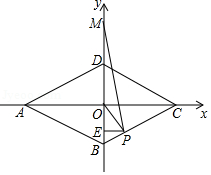
以菱形 的对角线交点 为坐标原点， 所在的直线为 轴，已知 ， ， ， 为折线 上一动点，作 轴于点 ，设点 的纵坐标为 ．
（1）求 边所在直线的解析式；
（2）设 ，求 关于 的函数关系式；
（3）当 为直角三角形时，求点 的坐标．
请把下列证明过程补充完整：
已知：如图，DE∥BC，BE平分∠ABC．求证：∠1=∠3．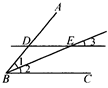
证明：因为BE平分∠ABC（已知），
所以∠1=______（）．
又因为DE∥BC（已知），
所以∠2=_____（）．
所以∠1=∠3（）．
解不等式组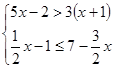
，并求出其整数解。
计算：
计算：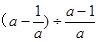
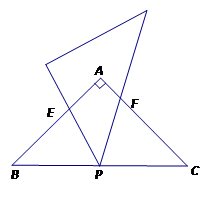
如图．等腰直角三角形ABC中，∠A=90°,P为BC的中点，小明拿着含45°角的透明三角形，使45°角的顶点落在点P，且绕P旋转．
（1）如图①：当三角板的两边分别AB、AC交于E、F点时，试说明△BPE∽△CFP．
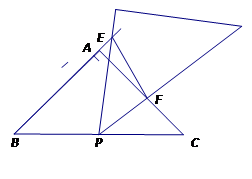
（2）将三角板绕点P旋转到图②，三角板两边分别交BA延长线和边AC于点EF．
探究1：△BPE与△CFP．还相似吗？（只需写结论）
探究2：连接EF，△BPE与△EFP是否相似？请说明理由．
