如果抛物线 的顶点在拋物线 上,抛物线 的顶点也在拋物线 上时,那么我们称抛物线 与 “互为关联”的抛物线.如图1,已知抛物线 与 是“互为关联”的拋物线,点 , 分别是抛物线 , 的顶点,抛物线 经过点 .
(1)直接写出 , 的坐标和抛物线 的解析式;
(2)抛物线 上是否存在点 ,使得 是直角三角形?如果存在,请求出点 的坐标;如果不存在,请说明理由;
(3)如图2,点 在抛物线 上,点 , 分别是抛物线 , 上的动点,且点 , 的横坐标相同,记 面积为 (当点 与点 , 重合时 , 的面积为 (当点 与点 , 重合时, ,令 ,观察图象,当 时,写出 的取值范围,并求出在此范围内 的最大值.

已知商场1~5月的商品销售总额一共是410万元.图①表示的是某综合商场今年1~5月的商品各月销售总额的情况,图②表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图①、图②,解答下列问题:
(1)请你根据这一信息将统计图补充完整;
(2)试求出商场服装部5月份的销售额;
(3)小刚观察图②后认为,5月份商场服装部的销售额比4月份减少了.他的看法正确吗?请说明理由.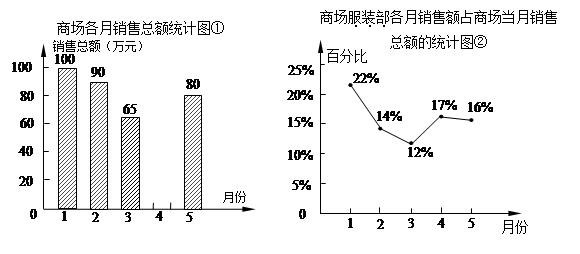
如图,在每格为1个单位的正方形网格中建立直角坐标系,反比例函数 的图象经过格点A.
的图象经过格点A.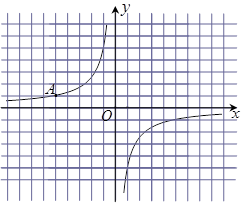
(1)请写出点A的坐标、反比例函数 的解析式;
的解析式;
(2)若点B(m,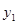 )、C(n,
)、C(n,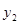 )(2<m<n)都在函数
)(2<m<n)都在函数 的图象上,试比较
的图象上,试比较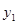 与
与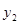 的大小.
的大小.
在一个黑色的布口袋里装着白、红两种颜色的小球,它们除了颜色之外没有其它区别,其中白球2个、红球1个,球在袋中进行搅匀.
(1)若随机地从袋中摸出1个球,则摸出红球的概率是多少?
(2)随机地从袋中摸出1个球,放回搅匀再摸出第二个球.请你用画树状图或列表的方法表示所有等可能的结果,并求两次都摸出白球的概率.
如图,已知AB=AC,AD=AE,∠1=∠2.求证:BD=CE.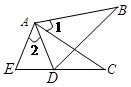
先化简,再求值: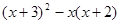 ,其中
,其中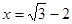 .
.